题目内容
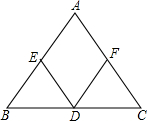
如图，在等腰△ABC的底边BC上任取一点D，作DE∥AC、DF∥AB，分别交AB、AC于点E、F，若等腰△ABC的腰长为m，底边长为n，则四边形AEDF的周长为（ ）
| A．2m | B．2n | C．m+n | D．2m-n |
∵AB=AC，
∴∠B=∠C，
∵DF∥AB，
∴∠B=∠FDC，
∴∠FDC=∠C，
∴DF=FC，
同理DE=BE，
∵DF∥AB，DE∥AC，
∴四边形AEDF是平行四边形，
∴?AEDF的周长=AE+DE+DF+AF=AE+BE+AF+CF=AB+AC=2AC=2m，
故选A．
∴∠B=∠C，
∵DF∥AB，
∴∠B=∠FDC，
∴∠FDC=∠C，
∴DF=FC，
同理DE=BE，
∵DF∥AB，DE∥AC，
∴四边形AEDF是平行四边形，
∴?AEDF的周长=AE+DE+DF+AF=AE+BE+AF+CF=AB+AC=2AC=2m，
故选A．
练习册系列答案
快捷英语周周练系列答案
相关题目
