题目内容
已知△ABC内接于⊙O,OD⊥AC于D,如果∠COD=32°,那么∠B的度数为( )
| A、16° | B、32° | C、16°或164° | D、32°或148° |
分析:等腰△AOC中,由于OD⊥AC,根据等腰三角形三线合一的特性可得OD平分顶角∠AOC.由此可求出∠AOC的度数.然后分两种情况讨论:
①∠B是锐角,此时∠B和圆心角∠AOC所对的弧相同,根据圆周角定理可求出∠B的度数;
②∠B是钝角,根据圆内接四边形的对角互补,可求出此时∠B的度数.
①∠B是锐角,此时∠B和圆心角∠AOC所对的弧相同,根据圆周角定理可求出∠B的度数;
②∠B是钝角,根据圆内接四边形的对角互补,可求出此时∠B的度数.
解答: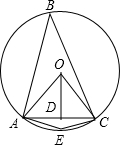 解:如图;
解:如图;
∵△OAC是等腰三角形,OD⊥AC,
∴OD是∠ADC的平分线,(等腰三角形三线合一)
∴∠AOC=2∠COD=64°;
①当点B在优弧AC上时,由圆周角定理知,∠B=
∠AOC=32°;
②当点B在如图点E的位置时,由圆内接四边形的对角互补知,∠E=180°-∠B=148°;
故选D.
 解:如图;
解:如图;∵△OAC是等腰三角形,OD⊥AC,
∴OD是∠ADC的平分线,(等腰三角形三线合一)
∴∠AOC=2∠COD=64°;
①当点B在优弧AC上时,由圆周角定理知,∠B=
| 1 |
| 2 |
②当点B在如图点E的位置时,由圆内接四边形的对角互补知,∠E=180°-∠B=148°;
故选D.
点评:本题考查垂弦定理、圆内接四边形的性质、圆心角、圆周角的应用能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.
如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.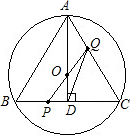 终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
 (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. (2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=
(2013•永州)如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=