题目内容
若关于x的方程ax2+2(a-b)x+(b-a)=0有两个相等的实数根,则a:b等于
- A.-1或2
- B.-2或1
- C.-
 或1
或1 - D.1或

D
分析:本题是根的判别式与解方程的综合应用,本题中根据根与系数的关系会出现关于a、b的二元二次方程,但是由于求解的结果是a:b,所以可以利用整体的思想进行求解.
解答:∵关于x的方程ax2+2(a-b)x+(b-a)=0有两个相等的实数根,
∴△=[2(a-b)]2-4×a×+(b-a)=0,
整理得2a2-3ab+b2=0,
即(2a-b)(a-b)=0
∴2a=b或a=b
a:b等于1或 .
.
故选D.
点评:本题根据方程有两个相等的实数根可以列出关于待定系数的方程,求解的时候可以利用整体的思想求出要求的整体,这是本题的难点.
分析:本题是根的判别式与解方程的综合应用,本题中根据根与系数的关系会出现关于a、b的二元二次方程,但是由于求解的结果是a:b,所以可以利用整体的思想进行求解.
解答:∵关于x的方程ax2+2(a-b)x+(b-a)=0有两个相等的实数根,
∴△=[2(a-b)]2-4×a×+(b-a)=0,
整理得2a2-3ab+b2=0,
即(2a-b)(a-b)=0
∴2a=b或a=b
a:b等于1或
 .
.故选D.
点评:本题根据方程有两个相等的实数根可以列出关于待定系数的方程,求解的时候可以利用整体的思想求出要求的整体,这是本题的难点.

练习册系列答案
相关题目
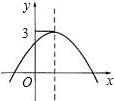 如图,是二次函数y=ax2+bx+c的图象,若关于x的方程ax2+bx+c-k=0有两个不相等的实数根,则k的取值范围是( )
如图,是二次函数y=ax2+bx+c的图象,若关于x的方程ax2+bx+c-k=0有两个不相等的实数根,则k的取值范围是( )| A、k<3 | B、k>3 | C、k≤3 | D、k≥3 |