题目内容
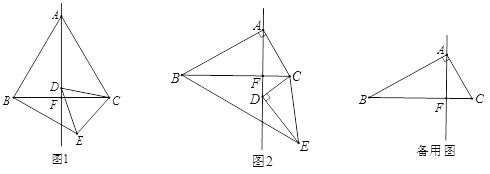
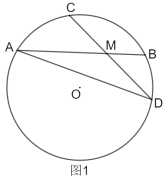
【题目】如图,AC,BD为四边形ABCD的对角线,AC⊥BC,AB⊥AD,CA=CD.若tan∠BAC=![]() .则tan∠DBC的值是( )
.则tan∠DBC的值是( )
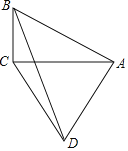
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据tan∠BAC=![]() ,得出∠BAC的度数,则在Rt△ACB中,设BC=1,则AC=
,得出∠BAC的度数,则在Rt△ACB中,设BC=1,则AC=![]() ;证明△CAD为等边三角形,过点D作DE⊥CA,交CA于点E,设CA与BD交于点F,则DE∥BC,从而∠DBC=∠FDE,设CF=x,则EF=
;证明△CAD为等边三角形,过点D作DE⊥CA,交CA于点E,设CA与BD交于点F,则DE∥BC,从而∠DBC=∠FDE,设CF=x,则EF=![]() ﹣x,根据tan∠DBC=tan∠FDE列出关于x的方程,解得x值,则可求得tan∠DBC的值.
﹣x,根据tan∠DBC=tan∠FDE列出关于x的方程,解得x值,则可求得tan∠DBC的值.
∵tan∠BAC=![]() ,
,
∴∠BAC=30°,
∵AC⊥BC,
∴∠ACB=90°,
∴设BC=1,则AC=![]() ,
,
∵AB⊥AD,
∴∠BAD=90°,
∴∠DAC=60°,
∵CA=CD,
∴△CAD为等边三角形,
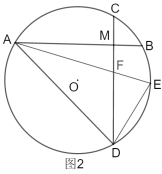
过点D作DE⊥CA,交CA于点E,设CA与BD交于点F,如图,
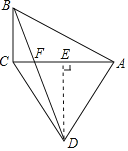
则有:CE=![]() AC=
AC=![]() ,DE=ADsin60°=
,DE=ADsin60°=![]() ×
×![]() =
=![]() ,
,
设CF=x,则EF=![]() ﹣x,
﹣x,
∵AC⊥BC,DE⊥CA,
∴DE∥BC,
∴∠DBC=∠FDE,
∴tan∠DBC=tan∠FDE,
∴![]()
∴![]() =
=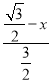 ,
,
解得:x=![]() ,
,
∴tan∠DBC=![]() =
=![]() .
.
故选:D.

练习册系列答案
相关题目