Question

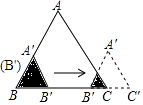
【题目】如图，在四边形ABCD中，AC、BD相交于点F，点E在BD上，且 = = ．
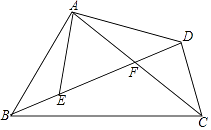
（1）试问：∠BAE与∠CAD相等吗？为什么？
（2）试判断△ABE与△ACD是否相似？并说明理由．

Answer 1

【答案】
（1）解：∠BAE与∠CAD相等．

理由：∵ = = ，

∴△ABC∽△AED，

∴∠BAC=∠EAD，

∴∠BAE=∠CAD

（2）解：△ABE与△ACD相似．

∵ = ，

∴ = ．

在△ABE与△ACD中，

∵ = ，∠BAE=∠CAD，

∴△ABE∽△ACD

【解析】（1）先根据题意得出△ABC∽△AED，由相似三角形的性质即可得出结论；（2）先根据题意得出 = ，再由∠BAE=∠CAD即可得出结论．
【考点精析】本题主要考查了相似三角形的判定的相关知识点，需要掌握相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）才能正确解答此题．