题目内容
在正方形ABCD中,∠EAF=45°,把△ADF绕着点A按顺时针方向旋转90°后,得到△ABM.试说明ME=EF.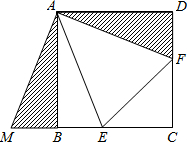

证明:∵△ADF绕着点A按顺时针方向旋转90°后,得到△ABM,
∴AM=AF,BM=DF,∠ABM=∠D=90°,∠FAM=90°,
而∠ABC=90°,
∴点M、B、E共线,
∵∠EAF=45°,
∴∠MAE=45°,
∵在△MAE和△FAE中
,
∴△MAE≌△FAE(SAS),
∴ME=EF.
∴AM=AF,BM=DF,∠ABM=∠D=90°,∠FAM=90°,
而∠ABC=90°,
∴点M、B、E共线,
∵∠EAF=45°,
∴∠MAE=45°,
∵在△MAE和△FAE中
|
∴△MAE≌△FAE(SAS),
∴ME=EF.

练习册系列答案
相关题目
 已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=
已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF= 18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
 如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.
如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.