题目内容
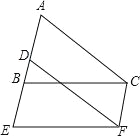
【题目】矩形ANCD中,AD=5,CD=3,在直线BC上取一点E,使△ADE是以DE为底的等腰三角形,过点D作直线AE的垂线,垂足为点F,则EF= .
【答案】9或1
【解析】解;如图1中, 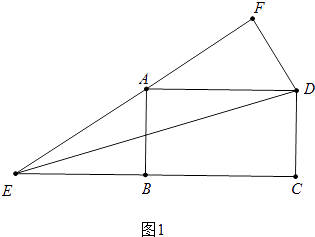
∵四边形ABCD是正方形,
∴AD=BC=5,AB=CD=3,∠ABC=∠C=∠ABE=90°,AD∥EC
∵AE=AD=5,
∴∠AED=∠ADE=∠DEC,
在RT△ABE中,∵AE=5,AB=3,
∴EB= ![]() =
= ![]() =4,
=4,
在△EDF和△EDC中,
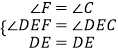 ,
,
△EDF≌△EDC
∴EF=EC=EB+BC=9.
如图2中, 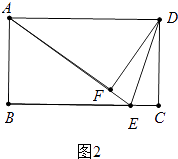
∵AD=AE=5,AB=3,
∴BE= ![]() =4,
=4,
∴EC=1,
∵AD∥BC,
∴∠ADE=∠DEC=∠AED,
在△EDF和△EDC中,
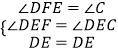 ,
,
∴△DEF≌△DEC,
∴EF=EC=1,
综上所述EF=9或1.
所以答案是9或1.
【考点精析】通过灵活运用等腰三角形的性质和勾股定理的概念,掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目