题目内容
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点M,使得无论k取何值, ![]() 为定值?若存在,求出点M的坐标;若不存在,请说明理由.
为定值?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】解:(I)由过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,
可知椭圆C过点 ![]() ,∴
,∴ ![]() ,
,
又∵e= ![]() =
= ![]() ,a2=b2+c2;
,a2=b2+c2;
三式联立解得 ![]() ,
,
∴椭圆的方程为 ![]() +y2=1;…(4分)
+y2=1;…(4分)
(II)设在x轴上存在点M(t,0)满足题意,
∵直线l过点(1,0)且斜率为k,则直线l的方程可设为:y=k(x﹣1);
由 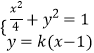 可知:x2+4k2(x﹣1)2=4,
可知:x2+4k2(x﹣1)2=4,
整理得(1+4k2)x2﹣8k2x+4k2﹣4=0;
易知:△=64k4﹣16(1+4k2)(k2﹣1)=16(3k2+1)>0;
设 A(x1 , y1),B(x2 , y2),
则:  ;
;
∴ ![]()
![]() =(x1﹣t,y1)(x2﹣t,y2)
=(x1﹣t,y1)(x2﹣t,y2)
=(x1﹣t)(x2﹣t)+y1y2
=x1x2﹣t(x1+x2)+t2+k2(x1﹣1)(x2﹣1)
=(1+k2)x1x2﹣(t+k2)(x1+x2)+t2+k2
= ![]() ;
;
由题意可设: ![]()
![]() ﹣
﹣ ![]() =m(m为常数),
=m(m为常数),
∴k2(4t2﹣8t)+t2﹣4=m+4mk2对任意实数k(k≠0)恒成立;
∴ ![]() ,解得:t=2,m=0;
,解得:t=2,m=0;
∴存在点M(2,0)满足题意,且常数为0.
【解析】(I)由题意知椭圆C过点 ![]() ,代入椭圆方程,再由离心率e以及a、b、c的关系列方程组求出a、b即可;(II)设在x轴上存在点M(t,0)满足题意,设出直线l的方程,与椭圆方程联立消去y,利用根与系数的关系得出x1+x2与x1x2 , 其中A(x1 , y1),B(x2 , y2);再计算
,代入椭圆方程,再由离心率e以及a、b、c的关系列方程组求出a、b即可;(II)设在x轴上存在点M(t,0)满足题意,设出直线l的方程,与椭圆方程联立消去y,利用根与系数的关系得出x1+x2与x1x2 , 其中A(x1 , y1),B(x2 , y2);再计算 ![]()
![]() ﹣
﹣ ![]() 的值,即可求出结论.
的值,即可求出结论.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案