题目内容
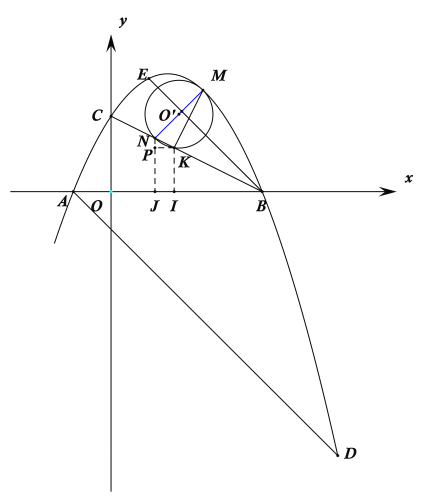
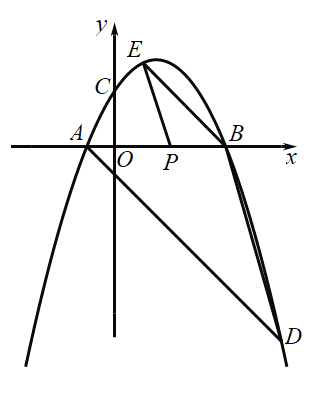
【题目】如图,在平面直角坐标系中,抛物线![]()
![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() ,且抛物线的对称轴经过点
,且抛物线的对称轴经过点![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,点
,点![]() 是该抛物线上一点,连接
是该抛物线上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直线![]() 及抛物线的函数表达式;
及抛物线的函数表达式;
(2)试问:![]() 轴上是否存在某一点
轴上是否存在某一点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() 为顶点的
为顶点的![]() 与
与![]() 相似?若相似,请求出此时点
相似?若相似,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() ,
,![]() 重合),过
重合),过![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,则
,则![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于_______.(直接写出答案)
上所截得的线段长度的最大值等于_______.(直接写出答案)
【答案】(1)![]() ;(2)相似,
;(2)相似,![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)由二次函数的对称性及B点坐标先求出点A的坐标,代入![]() 中求出AD的解析式即可,再将A、B点坐标代入二次函数解析式中,结合对称轴
中求出AD的解析式即可,再将A、B点坐标代入二次函数解析式中,结合对称轴![]() 联立方程组求出二次函数解析式.
联立方程组求出二次函数解析式.
(2)先计算出 ![]() ,此时AD∥BE,再分情况讨论P点在B点左侧和P点在B点右侧时的情形.
,此时AD∥BE,再分情况讨论P点在B点左侧和P点在B点右侧时的情形.
(3) 设![]() 在直线
在直线![]() 上所截得的线段为NK,过K点作KI⊥x轴于I点,NJ⊥x轴于J点,PK⊥NJ于P点,设M点的坐标为(
上所截得的线段为NK,过K点作KI⊥x轴于I点,NJ⊥x轴于J点,PK⊥NJ于P点,设M点的坐标为(![]() ),将N,K坐标分别用m的代数式表示,最后利用
),将N,K坐标分别用m的代数式表示,最后利用![]() 即可求解.
即可求解.
(1)由题可知,对称轴:![]() ,点
,点![]()
则点![]()
![]() 得
得![]()
![]() 直线
直线![]()
由题可得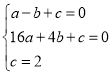
解得![]() ,
,![]() ,
,![]()
![]() 抛物线的函数关系式
抛物线的函数关系式![]()
(2)![]() 点
点![]() 在抛物线上
在抛物线上
![]() 即
即![]()
易求得直线![]()
由题可得: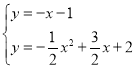
![]() 直线
直线![]() 交抛物线于点
交抛物线于点![]() ,
,![]()
可知,![]()
则:![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
设![]()
①若点![]() 在点
在点![]() 左侧时
左侧时
![]()
(i)当![]() 时
时
则![]()
即:![]()
![]()
即:点![]()
(ii)当![]() 时
时
则![]()
即:![]()
![]()
即:点![]()
②若点![]() 在点
在点![]() 右侧时
右侧时
![]() ,
,
又![]()
![]()
此时,![]() 与
与![]() 不相似
不相似
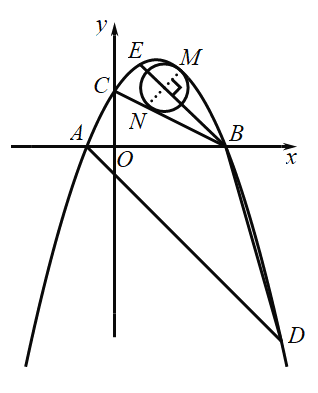
(3)![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于
上所截得的线段长度的最大值等于![]() ,如下图所示:
,如下图所示:
设![]() 在直线
在直线![]() 上所截得的线段为NK,过K点作KI⊥x轴于I点,NJ⊥x轴于J点,PK⊥NJ于P点,
上所截得的线段为NK,过K点作KI⊥x轴于I点,NJ⊥x轴于J点,PK⊥NJ于P点,
设M点坐标为(![]() )
)
∵BE⊥MN,∴![]() ,且
,且![]()
∴![]()
∴直线MN的解析式为:![]() ,与直线BC联立方程组:
,与直线BC联立方程组:
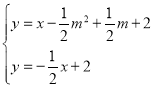
解得N点坐标为![]()
∵MN是圆O的直径,∴∠MKN=90°
∴MK⊥BC,即![]() ,且
,且![]()
∴直线MK的解析式为:![]() ,与直线BC联立方程组:
,与直线BC联立方程组:
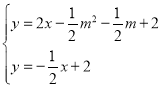
解得K点坐标为![]()
由图像可知,![]()
∴![]()
∴当![]() 时,
时,![]() 最大值等于
最大值等于![]() .
.
故答案为:![]() .
.