题目内容
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.

(1)求直线![]() 和反比例函数
和反比例函数![]() 的解析式;
的解析式;
(2)已知点![]() 是反比例函数
是反比例函数![]() 图象上的一个动点,求点
图象上的一个动点,求点![]() 到直线
到直线![]() 距离最短时的坐标.
距离最短时的坐标.
【答案】(1)![]() ;(2)
;(2)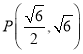
【解析】
(1)将点A(1,0),点B(0,2),代入y=mx+b,可求直线解析式;过点C作CD⊥x轴,根据三角形全等可求C(3,1),进而确定k;
(2)设与AB平行的直线y=-2x+h,联立-2x+h=![]() ,当△=h2-24=0时,点P到直线AB距离最短;
,当△=h2-24=0时,点P到直线AB距离最短;
解:(1)将点![]() ,点
,点![]() ,代入
,代入![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵过点![]() 作
作![]() 轴,
轴,
∵线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,
,
∴![]() ≌
≌![]() (
(![]() ),
),
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
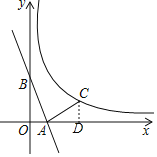
(2)设与![]() 平行的直线
平行的直线![]() ,
,
联立![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,此时点
,此时点![]() 到直线
到直线![]() 距离最短;
距离最短;
∴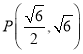 ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
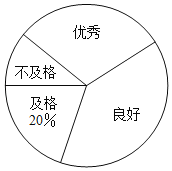
【题目】某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
成绩等级 | 频数(人) | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.