Question

如图，已知线段AB。

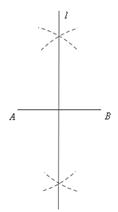
（1）用尺规作图的方法作出线段AB的垂直平分线l（保留作图痕迹，不要求写出作法）；
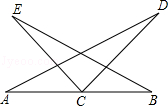
（2）在（1）中所作的直线l上任意取两点M、N（线段AB的上方），连接AM、AN。BM、BN。
求证：∠MAN=∠MBN。

Answer 1

解：（1）作图如下：

（2）证明：根据题意作出图形如图，

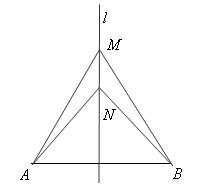
∵点M、N在线段AB的垂直平分线l上，
∴AM=BM，AN=BN。
又 ∵MN=MN，∴△AMN≌△BMN（SSS）。
∴∠MAN=∠MBN。

（1）根据线段垂直平分线的性质作图。
（2）根据线段垂直平分线上的点到线段两端距离相等的性质，可得AM=BM，AN=BN。MN是公共边，从而SSS可证得△AMN≌△BMN，进而得到∠MAN=∠MBN的结论。