题目内容
如图:已知D、E分别在AB、AC上,AB=AC,∠B=∠C,求证:BE=CD.
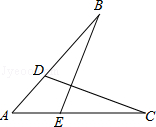

证明:在△ABE和△ACD中,
∵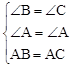 ,∴△ABE≌△ACD(AAS)。
,∴△ABE≌△ACD(AAS)。
∴BE=CD(全等三角形的对应边相等)。
∵
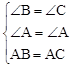 ,∴△ABE≌△ACD(AAS)。
,∴△ABE≌△ACD(AAS)。∴BE=CD(全等三角形的对应边相等)。
要证明BE=CD,把BE与CD分别放在两三角形中,证明两三角形全等即可得到,而证明两三角形全等需要三个条件,题中已知一对边和一对角对应相等,观察图形可得出一对公共角,进而利用AAS可得出三角形ABE与三角形ACD全等,利用全等三角形的对应边相等可得证。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

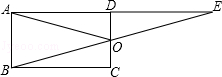
 中,对角线AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有【 】
中,对角线AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有【 】
 EF的长半径画弧,两弧交于点G;作射线AG交CD于点H。则下列结论:
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H。则下列结论: