题目内容
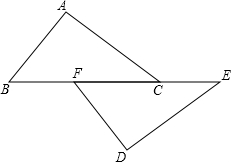
如图,C是AB的中点,AD=BE,CD=CE.
求证:∠A=∠B.
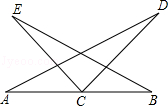
求证:∠A=∠B.

证明:∵C是AB的中点,∴AC=BC。
在△ACD和△BCE中,∵AD=BE,CD=CE.AC=BC,
∴△ACD≌△BCE(SSS)。
∴∠A=∠B。
在△ACD和△BCE中,∵AD=BE,CD=CE.AC=BC,
∴△ACD≌△BCE(SSS)。
∴∠A=∠B。
试题分析:根据中点定义求出AC=BC,然后利用“SSS”证明△ACD和△BCE全等,再根据全等三角形对应角相等证明即可。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目