Question

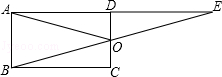
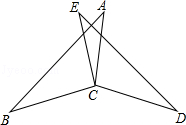
如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E；
求证：BC=DC．

Answer 1

证明：∵∠BCE=∠DCA，
∴∠BCE+∠ACE=∠DCA+∠ACE，即∠ACB=∠ECD。
在△ABC和△EDC中，
∵，
∴△ABC≌△EDC（ASA）。∴BC=DC

试题分析：先求出∠ACB=∠ECD，再利用“角边角”证明△ABC和△EDC全等，然后根据全等三角形对应边相等证明即可。