题目内容
如图，在矩形ABCD中，AB=16cm，AD=8cm，把△BCD沿对角线BD翻折，使点C落在点E处，DE交AB于点F．
（1）求证：BF=DF；
（2）求△BDF的面积．
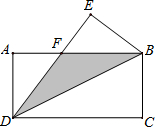
（1）求证：BF=DF；
（2）求△BDF的面积．
（1）证明：由折叠的性质可得：∠EDB=∠CDB，
∵AB∥CD，
∴∠CDB=∠ABD，
∴∠FDB=∠FBD，
∴BF=DF．
（2）设BF=DF=x，则AF=16-x，
在Rt△ADF中，AF2+AD2=DF2，即（16-x）2+82=x2，
解得：x=10，
故S△BDF=
BF×AD=40cm2．
∵AB∥CD，
∴∠CDB=∠ABD，
∴∠FDB=∠FBD，
∴BF=DF．
（2）设BF=DF=x，则AF=16-x，
在Rt△ADF中，AF2+AD2=DF2，即（16-x）2+82=x2，
解得：x=10，
故S△BDF=
| 1 |
| 2 |
练习册系列答案
寒假学与练系列答案
相关题目
