题目内容
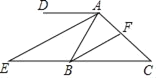
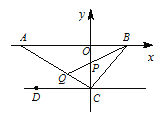
【题目】如图 ,CE 平分∠ACD,AE 平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
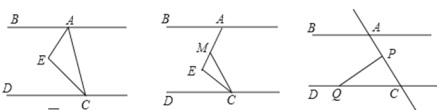
(2)如图,在(1)的结论下,当∠E=90°保持不变时,移动直角顶点 E,使∠MCE=∠ECD, 当直角顶点 E 点移动时,请确定∠BAE 与![]() ∠MCD 的数量关系,并说明理由;
∠MCD 的数量关系,并说明理由;
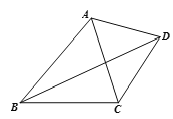
(3)如图,在(1)的结论下,P 为线段 AC 上的一个定点,点 Q 为直线 CD 上的一个动点,当点 Q 在射线 CD 上运动时(点 C 除外)∠BAC 与∠CPQ+∠CQP 有何数量关系?为什么?
【答案】(1)AB∥CD,理由见解析;(2)∠BAE+![]() ∠MCD =90°,理由见解析;(3)∠BAC =∠CPQ+∠CQP,理由见解析
∠MCD =90°,理由见解析;(3)∠BAC =∠CPQ+∠CQP,理由见解析
【解析】
(1)根据角平分线定义得出∠ACD=2∠ACE,∠BAC=2∠EAC,求出∠ACD+∠BAC=180°,根据平行线的判定即可得出结论;
(2)作EF∥AB,易得EF∥CD∥AB,根据平行线的性质得出∠BAE=∠AEF, ∠FEC=∠ECD,再由∠AEF+∠FEC=90°,通过等量代换后即可得出结论;
(3)作PM∥AB,易得PM∥CD∥AB,根据平行线的性质得出∠BAC=∠MPC,∠MPQ=∠CQP,由∠MPC=∠MPQ+∠CPQ,通过等量代换后即可得出结论.
(1)AB∥CD,理由如下:
∵CE 平分∠ACD,AE 平分∠BAC,
∴∠ACD=2∠ACE,∠BAC=2∠EAC,
又∵∠EAC+∠ACE=90°
∴∠ACD+∠BAC=2(∠ACE+∠EAC)=180°
∴AB∥CD
(2)∠BAE+![]() ∠MCD =90°,理由如下:
∠MCD =90°,理由如下:
如图所示,作EF∥AB,
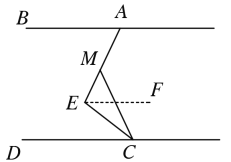
∵AB∥CD
∴EF∥CD∥AB
∴∠BAE=∠AEF,∠FEC=∠ECD
∵∠E=90°,即∠AEF+∠FEC=90°
∴∠BAE+∠ECD=90°
又∵∠MCE=∠ECD
∴∠ECD=![]() ∠MCD
∠MCD
∴∠BAE+![]() ∠MCD =90°
∠MCD =90°
(3)∠BAC =∠CPQ+∠CQP,理由如下:
如图所示,作PM∥AB,
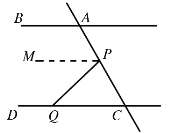
∵AB∥CD
∴PM∥CD∥AB
∴∠BAC=∠MPC,∠MPQ=∠CQP,
又∵∠MPC=∠MPQ+∠CPQ,
∴∠BAC=∠MPC=∠CQP+∠CPQ
即∠BAC =∠CPQ+∠CQP

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案