题目内容
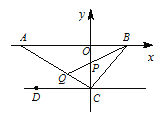
【题目】如图, A为x轴负半轴上一点, B为x轴正半轴上一点, C(0,-2),D(-3,-2).
(1)求△BCD的面积;
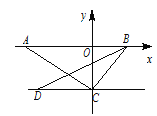
(2)若AC⊥BC,作∠CBA的平分线交CO于P,交CA于Q,判断∠CPQ与∠CQP的大小关系, 并证明你的结论.
【答案】(1)3;(2)∠CPQ=∠CQP,理由见解析;
【解析】
(1)求出CD的长度,再根据三角形的面积公式列式计算即可得解;
(2)根据角平分线的定义可得∠ABQ=∠CBQ,然后根据等角的余角相等解答;
解:(1)∵点C(0,-2),D(-3,-2),
∴CD=3,且CD//x轴
∴△BCD面积=![]() ×3×2=3;
×3×2=3;
(2)∠CPQ=∠CQP,
∵AC⊥BC,
∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°
∴∠OAC=∠BCO,又BQ平分∠CBA,
∴∠ABQ=∠CBQ,
∵∠CQP=∠OAC+∠ABQ
∠CPQ=∠CBQ+∠BCO,
∴∠CQP=∠CPQ
(2)∠CPQ=∠CQP,
∵AC⊥BC,
∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°
∴∠OAC=∠BCO,又BQ平分∠CBA,
∴∠ABQ=∠CBQ,
∵∠CQP=∠OAC+∠ABQ
∠CPQ=∠CBQ+∠BCO,
∴∠CQP=∠CPQ

练习册系列答案
相关题目