题目内容
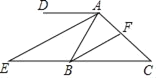
【题目】如图,AD∥EC.
(1)若∠C=40°,AB平分∠DAC,求∠DAB的度数.
(2)若AE平分∠DAB,BF平分∠ABC,试说明AE∥BF的理由.
【答案】(1)70°;(2)证明见解析
【解析】
(1)已知AD∥EC,根据两直线平行,同旁内角互补可得∠C+∠DAC=180°,即可求得∠DAC=140°,再根据角平分线的定义即可求得∠DAB=![]() ∠DAC=70°;(2)已知AD∥EC,根据两直线平行,内错角相等可得∠DAB=∠ABC;已知AE平分∠DAB,BF平分∠ABC,根据角平分线的定义可得∠EAB=
∠DAC=70°;(2)已知AD∥EC,根据两直线平行,内错角相等可得∠DAB=∠ABC;已知AE平分∠DAB,BF平分∠ABC,根据角平分线的定义可得∠EAB=![]() ∠DAB,∠ABF=
∠DAB,∠ABF=![]() ∠ABC,所以∠EAB=∠ABF,根据内错角相等,两直线平行即可判定AE∥BF.
∠ABC,所以∠EAB=∠ABF,根据内错角相等,两直线平行即可判定AE∥BF.
(1)∵AD∥EC,
∴∠C+∠DAC=180°,
∵∠C=40°,
∴∠DAC=140°,
∵AB平分∠DAC,
∴∠DAB=![]() ∠DAC=70°;
∠DAC=70°;
(2)理由是:∵AD∥EC,
∴∠DAB=∠ABC,
∵AE平分∠DAB,BF平分∠ABC,
∴∠EAB=![]() ∠DAB,∠ABF=
∠DAB,∠ABF=![]() ∠ABC,
∠ABC,
∴∠EAB=∠ABF,
∴AE∥BF.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目