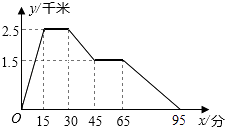
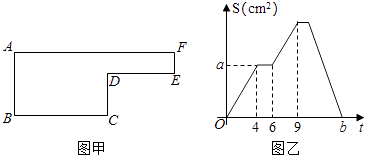
题目内容
【题目】（本题满分10分）
如图，在直角坐标平面内，已知点A（8，0），点B（3，0），点C是点A关于直线m（直线m上各点的横坐标都为3）的对称点．
（1）在图中标出点A，B，C的位置，并求出点C的坐标；
（2）如果点P在y轴上，过点P作直线l∥x轴，点A关于直线l的对称点是点D，那么当△BCD的面积等于15时，求点P的坐标．
【答案】（1）（﹣2，0）；(2) （0，3）或（0，﹣3）
【解析】试题分析：(1)直接点A，B的位置标注即可，根据题意可得直线m为直线x=3，由点C是点A关于直线m对称，求得点C的坐标，再标注即可；（2）根据题意作出图形，根据三角形的面积公式求得△BCD△边BC的高，即可求得OP的长，即可得点P的坐标.
试题解析：
（1）三个点位置标注正确
点C的坐标为（﹣2，0）；
（2）如图，由题意知,S△BCD=
BCAD=15，BC=5，∴AD=6，则OP=3，
∴点P的坐标为（0，3）或（0，﹣3）．
练习册系列答案
相关题目
