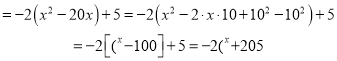题目内容
【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（1，0），（0，2），某抛物线的顶点坐标为D（﹣1，1）且经过点B，连接AB，直线AB与此抛物线的另一个交点为C，则S△BCD：S△ABO=（ ）
A.8：1
B.6：1
C.5：1
D.4：1
【答案】B
【解析】
试题分析：设直线AB的解析式为y=kx+b，二次函数的解析式为y=a（x+1）2+1，
将点A（1，0）、B（0，2）代入y=kx+b中得：
，解得：
，
∴直线AB的解析式为y=﹣2x+2；
将点B（0，2）代入到y=a（x+1）2+1中得：
2=a+1，解得：a=1，
∴二次函数的解析式为y=（x+1）2+1=x2+2x+2.
将y=﹣2x+2代入y=x2+2x+2中得：
﹣2x+2=x2+2x+2，整理得：x2+4x=0，
解得：x1=﹣4，x2=0，
∴点C的坐标为（﹣4，10）.
∵点C（﹣4，10），点B（0，2），点A（1，0），
∴AB=
，BC=
，
∴BC=4AB.
∵直线AB解析式为y=﹣2x+2可变形为2x+y﹣2=0，
∴|﹣2+1﹣2|=3，|﹣2|=2.
∴S△BCD：S△ABO=4×3：2=12：2=6：1.
故选B.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
