题目内容
【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?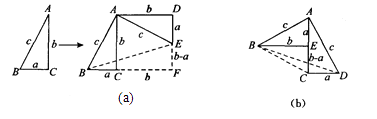
【答案】解:方法1:∵由图(a)可知S正方形ACFD=S四边形ABFE ,
∴S正方形ACFD=S⊿BAE+S⊿BFE
又∵正方形ACFD的边长为b, SRt△BAE= ![]() ,SRt△BFE=
,SRt△BFE= ![]()
∴b2 = ![]() +
+ ![]()
即2b2 =c2 +(b+a)(b-a)
整理得: a2 +b2=c2
方法2:如图(b)中,Rt△BEA和Rt△ACD全等, 设CD=a,AC=b,AD=c(b>a),
则AE=a,BE=b,AB=c,EC=b-a
由图(b),S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD
又∵ SRt△BAE = ![]() , SRt△ACD =
, SRt△ACD = ![]() ,SRt△BEC =
,SRt△BEC = ![]() ,
,
SRt△BAD= ![]() ,S△BCD=
,S△BCD= ![]() ,
,
∴ ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]()
即2ab+b(b-a) = c2 +a(b-a)
整理得: a2 +b2=c2
【解析】方法1:由S正方形ACFD=S⊿BAE+S⊿BFE,从而列出方程进行解答即可;
(2)方法2:由S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD,列方程解答即可。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目