��Ŀ����
����Ŀ��ΪԤ������H1N1���У�ijУ�Խ�������ҩ�������������֪����ҩ��ʱÿ���������еĺ�ҩ��y�����ˣ���ʱ��x�����ӣ������ȣ�ҩ���������y��x�ɷ���������ͼ��ʾ�����ֲ��10���������������ÿ�����ĺ�ҩ��Ϊ8���ˣ�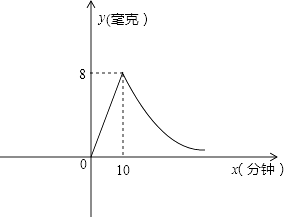
��1��������ҩ��ʱ���������y����x�ĺ�����ϵʽ��
��2����������ÿ�����ĺ�ҩ������2����ѧ�����ɽ����ң���������ʼ������Ҫ�������ٷ��ӣ�ѧ�����ܻص����ң�
��3�����������ÿ�����ĺ�ҩ��������4���ˣ��ҳ���ʱ�䲻����10����ʱ������ɱ�����в�������ô�˴������Ƿ���Ч��Ϊʲô��
���𰸡�
��1���⣺�١ߵ�0��x��10ʱy��x����������
�����y=kx��
�ߵ�x=10ʱ��y=8��
��8=10k��
��k= ![]() ��
��
�� ![]() ��0��x��10����
��0��x��10����
�ڡߵ�x��10ʱy��x�ɷ�������
����� ![]() ��
��
�ߵ�x=10ʱ��y=8��
�� ![]() ��
��
��k=80��
�� ![]() ��x��10����
��x��10����
��2���⣺��y��2ʱ���� ![]() ��
��
���x��40��
��������ʼ������Ҫ����40���ӣ�ѧ�����ܻص����ң�
��3���⣺��y=4���� ![]() �У���x=5��
����x=5��
��y=4���� ![]() ����x=20��
����x=20��
��20��5=15��10��
�౾��������Ч��
����������1���۲�ͼ���֪���١ߵ�0��x��10ʱy��x�����������ڡߵ�x��10ʱy��x�ɷ����������ô���ϵ�����������������뼴������������Ľ���ʽ��
��2��������֪������ÿ�����ĺ�ҩ������2����ѧ�����ɽ����ң�Ҫ��������⣬Ӧ�ÿ�����������������y��2ʱ����Ϸ��������������x��ȡֵ��Χ���ɣ�
��3���ֱ�y=4��������������ʽ�����Ӧ��x��ֵ������������ǵIJ��10�Ƚϴ�С���ɡ�