Question

【题目】如图，在□ABCD中，按以下步骤作图：①以点A为圆心，AB的长为半径作弧，交AD于点F;②分别以点F，B为圆心大于FB的长为半径作弧，两弧在∠DAB内交于点G;③作射线AG，交边BC于点E，连接EF．若AB=5，BF=8，则四边形ABEF的面积为（ ）

A.12B.20C.24D.48

Answer 1

【答案】C

【解析】

如图，设AE交BF于点O．证明四边形ABEF是菱形，利用勾股定理求出OA即可得出AE, 根据菱形的面积等于对角线乘积的一半即可解决问题．

解：如图，设AE交BF于点O．

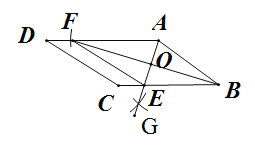
由作图可知：AB=AF，AE⊥BF，
∴OB=OF，∠BAE=∠EAF，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EAF=∠AEB，
∴∠BAE=∠AEB，
∴AB=BE=AF，∵AF∥BE，
∴四边形ABEF是平行四边形，
∵AB=AF，
∴四边形ABEF是菱形，
∴OA=OE，OB=OF=4，
在Rt△AOB中，∵∠AOB=90°，

∴AE=2OA=6．
∴菱形ABEF的面积=×8×6=24

故选：C．