题目内容
【题目】“面积法”是指利用图形面积间的等量关系寻求线段间等量关系的一种方法．例如：在△ABC中，AB＝AC，点P是BC所在直线上一个动点，过P点作PD⊥AB、PE⊥AC，垂足分别为D、E，BF为腰AC上的高．如图①，当点P在边BC上时，我们可得如下推理：
∵S△ABC＝S△ABP+S△ACP
∴
ACBF＝ABPD+ACPE
∵AB＝AC
∴ACBF＝AC（PD+PE）
∴BF＝PD+PE
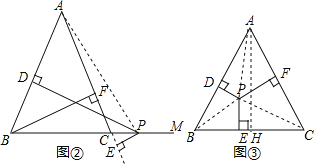
（1）（变式）如图②，在上例的条件下，当点P运动到BC的延长线上时，试探究BF、PD、PE之间的关系，并说明理由．
（2）（迁移）如图③，点P是等边△ABC内部一点，作PD⊥AB、PE⊥BC、PF⊥AC，垂足分别为D、E、F，若PD＝1，PE＝2，PF＝4．求△ABC的边长．
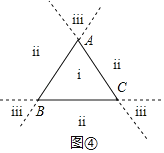
（3）（拓展）若点P是等边△ABC所在平面内一点，且点P到三边所在直线的距离分别为2、3、6．请直接写出等边△ABC的高的所有可能
【答案】（1）BF＝PD﹣PE，理由见解析；（2）
；（3）11，7，5，1．
【解析】
（1）如图②，连接AP，根据S△ABC＝S△ABP﹣S△ACP列式，即可得到结论；
（2）如图③，过A作AH⊥BC于H，连接PA，PB，PC，根据面积法求出AH＝PD＋PE＋PF＝7，然后根据等边三角形的性质得到CH＝
BC＝AC，在Rt△AHC中利用勾股定理构建方程即可得到结论；
（3）如图④，设等边△ABC的高为h，点P到△ABC的三边的距离为h1＝2，h2＝3，h3＝6，分三种情况讨论即可得到结论．
解：（1）BF＝PD﹣PE，
如图②，连接AP，
∵S△ABC＝S△ABP﹣S△ACP，
∴ACBF＝ABPD﹣ACPE，
∵AB＝AC，
∴BF＝PD﹣PE；
（2）如图③，过A作AH⊥BC于H，连接PA，PB，PC，
∵S△ABC＝S△ABP+S△ACP+S△BCP，即AHBC＝PDAB+PFAC+PEBC，
∵△ABC是等边三角形，
∴AB＝AC＝BC，
∴AH＝PD+PE+PF＝7，
∵AB＝AC，AH⊥BC，
∴CH＝BC＝AC，
在Rt△AHC中，∠AHC＝90°，
∴AH2+CH2＝AC2，即49＋
AC2＝AC2，
∴AC＝
＝；
（3）如图④，设等边△ABC的高为h，点P到△ABC的三边的距离为h1＝2，h2＝3，h3＝6，
当P在i区域时，由（2）可得h＝h1+h2+h3＝2+3+6＝11；
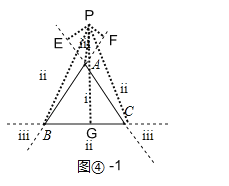
当P在iii区域时，如图④－1，PF＝h1＝2，PE＝h2＝3，PG＝h3＝6，连接
∵S△ABC＝S△PBC－S△ACP－S△ABP＝hBC＝PGBC－PEAC－PFAB，
∵AB＝AC＝BC，
∴h＝h3﹣h2﹣h1＝1，
当P在ii区域时，同理可得h＝h1+h3﹣h2＝2+6﹣3＝5或h＝h2+h3﹣h1＝3+6﹣2＝7，
综上所述，等边△ABC的高的所有可能的值为11，1，7，5．
