题目内容
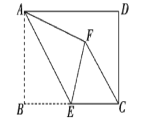
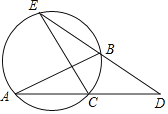
【题目】如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为
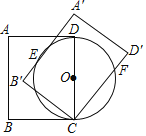
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD=5、BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=2.5,继而求得CG=B′E=OH=![]() ,根据垂径定理可得CF的长.
,根据垂径定理可得CF的长.
连接OE,延长EO交CD于点G,作OH⊥B′C于点H,
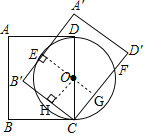
则∠OEB′=∠OHB′=90°,
∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,
∴∠B′=∠B′CD′=90°,AB=CD=5、BC=B′C=4,
∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=2.5,
∴B′H=OE=2.5,
∴CH=B′C-B′H=1.5,
∴CG=B′E=OH=![]() ,
,
∵四边形EB′CG是矩形,
∴∠OGC=90°,即OG⊥CD′,
∴CF=2CG=4,
故选C.

练习册系列答案
相关题目