Question

【题目】(1)如图，用尺规作图的方法作出的角平分线. (保留作图痕迹，不要求写出作法)

(2)在(1)的基础上证明命题“全等三角形的对应角角平分线相等”是真命题.请填空并证明.

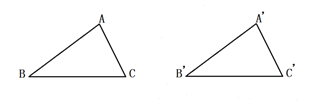
已知：如图，__________________，和分别是和的平分线.

求证：______________________________.

证明：

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据角平分线的作图方法解答即可；

（2）作出图形，结合图形写出已知、求证，由全等三角形的性质和角平分线的定义可得∠BAD=∠B'A'D'，根据ASA可得△ABD和△A'B'D'全等，所以角平分线AD、A'D'相等．

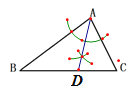
（1）如图，

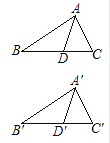
（2）已知：如图，△ABC≌△A′B′C′，AD、A′D′是∠BAC和∠B′A′C′的平分线，

求证：AD=A′D′．

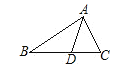
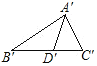
证明：∵△ABC≌△A′B′C′，

∴∠B=∠B′，AB=A′B′，∠BAC=∠B′A′C′，

∵AD平分∠BAC，A′D′平分∠B'A'C'，

∴∠BAD=∠B′A′D′，

在△ABD和△A′B′D′中，

∵∠B=∠B′，

AB=A′B′，

∠BAD=∠B′A′D′，

∴△ABD≌△A′B′D′（ASA），

∴AD=A′D′．