Question

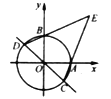
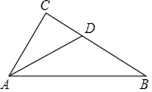
【题目】已知：如图，在Rt△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D．

（1）以AB边上一点O为圆心，过A、D两点作⊙O，并标出圆心．（不写作法，保留作图痕迹）．

（2）判断直线BC与⊙O的位置关系，并说明理由．

（3）若AB＝8，BD＝4，求⊙O的半径．

Answer 1

【答案】（1）作图见解析；（2）直线BC与⊙O的位置关系为：相切；理由见解析；（3）⊙O的半径为3．

【解析】

（1）以AB边上一点O为圆心，过A、D两点作⊙O，并标出圆心；

（2）根据切线的判定即可判断直线BC与⊙O的位置关系；

（3）根据AB=8，BD=4，即可求⊙O的半径．

（1）如图，⊙O即为所求；

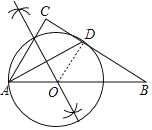
（2）直线BC与⊙O的位置关系为：相切，理由如下：

连接OD，

∴OD＝OA，

∴∠OAD＝∠ODA，

∵AD平分∠BAC，

∴∠BAD＝∠CAD，

∴∠ODA＝∠CAD，

∴AC∥OD，

∴∠ODB＝∠C＝90°，

∴OD⊥BC，OD是半径，

∴直线BC与⊙O相切；

（3）设⊙O的半径为x，

在Rt△OBD中，OD＝x，OB＝8﹣x，BD＝4，

∴（8﹣x）2＝x2+42，

解得x＝3．

答：⊙O的半径为3．