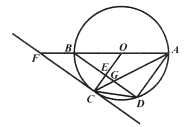
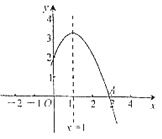
题目内容
【题目】某教学网站策划了![]() 、
、![]() 两种上网学习的月收费方式:
两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 月包时上网时间/ | 月超时费/(元/ |
| 7 | 25 | 0.6 |
| 10 | 50 | 3 |
设每月上网学习的时间为![]() .
.
(Ⅰ)根据题意,填写下表:
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | ||
方式 | 10 | 45 |
(Ⅱ)设![]() ,
,![]() 两种方式的收费金额分别为
两种方式的收费金额分别为![]() 元和
元和![]() 元,分别写出
元,分别写出![]() ,
,![]() 与
与![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,你认为哪种收费方式省钱?请说明理由.
时,你认为哪种收费方式省钱?请说明理由.
【答案】(Ⅰ)见解析,(Ⅱ)![]() (Ⅲ)当
(Ⅲ)当![]() 时,收费方式A省钱
时,收费方式A省钱
【解析】
(Ⅰ)首先判断月包时上网时间和月上网时间的大小,然后根据月总费用=月使用费+超时单价×超过时间,进行计算即可
(Ⅱ)根据收取费用=月使用费+超时单价×超过时间,可得出![]() 关于x的函数关系式,注意进行分段;
关于x的函数关系式,注意进行分段;
(Ⅲ)当![]() 时,根据(Ⅱ)的解析式,求出
时,根据(Ⅱ)的解析式,求出![]() 与
与![]() 的差,根据一次函数的增减性得出省钱的收费方式.
的差,根据一次函数的增减性得出省钱的收费方式.
(Ⅰ)见表格
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | 12 | 19 |
方式 | 10 | 45 | 0 | 10 |
(Ⅱ)当0![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
∴![]() ;
;
当0![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() ;
;
(Ⅲ)当![]() 时,收费方式A省钱
时,收费方式A省钱
当![]() 时,
时,![]() ,
,![]() ;
;
设y=![]()
∵-2.4![]() ,∴y随x的增大而减小
,∴y随x的增大而减小
当x=60时,y=-12,
∴当![]() 时,y
时,y![]() ,即y
,即y![]()
∴![]()
∴当![]() 时,收费方式A省钱.
时,收费方式A省钱.

 灵星计算小达人系列答案
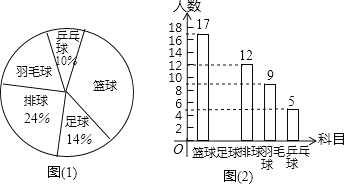
灵星计算小达人系列答案【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.