题目内容
已知，如图，四边形ABCD中，AB⊥BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积。
连接AC，∵∠B=90°，AB=1，BC=2，
∴AC=
在△ACD中，
AC2+CD2=5+4=9=AD2，
∴△ACD是直角三角形，
∴S四边形ABCD=
AB•BC+AC•DC=×1×2+×
×2=1+．
答：四边形ABCD的面积是1+．
∴AC=
在△ACD中，AC2+CD2=5+4=9=AD2，
∴△ACD是直角三角形，
∴S四边形ABCD=
AB•BC+AC•DC=×1×2+××2=1+．答：四边形ABCD的面积是1+
．先根据勾股定理求出AC的长度，再根据勾股定理的逆定理判断出△ACD的形状，再利用三角形的面积公式求解即可
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
，BE=2
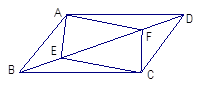
，AB=CD=AD=2，
，则下底BC长是
、
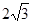
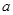，将这两个正方形拼在一起．问能否将此图适当分割，重新拼成一个正方形，使其面积等于已知两个正方形面积的和：
