题目内容
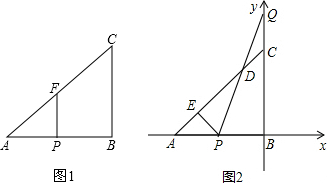
如图1,在△ABC中,∠B=90°,AB=BC=2,点P从A出发沿线段AB运动,过点P作PF∥BC,交线段AC于点F.
(1)点P在运动的过程中,△APF的形状
(2)如图2以顶点B为坐标原点,线段AB所在直线为x轴,建立平面直角坐标系,点P从A出发的同时,点Q从C出发沿BC的延长线运动,它们的运动速度相同,连线PQ与边AC交于点D.试解决以下两个问题:
①当AP为何值时,S△PCQ=
S△ABC;
②作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
(1)点P在运动的过程中,△APF的形状
不变
不变
(填“改变”或“不变”).如果改变,请指出所有可能出现的形状;如果不变,请指出它是什么三角形.答:等腰直角三角形
等腰直角三角形
.(2)如图2以顶点B为坐标原点,线段AB所在直线为x轴,建立平面直角坐标系,点P从A出发的同时,点Q从C出发沿BC的延长线运动,它们的运动速度相同,连线PQ与边AC交于点D.试解决以下两个问题:
①当AP为何值时,S△PCQ=
| 1 | 4 |
②作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.

分析:(1)根据等腰直角三角形的性质求出∠A=∠C=45°,根据两直线平行,同位角相等求出∠AFP=∠C=45°,从而判断出△APF是等腰直角三角形;
(2)①设AP=CQ=x,表示出PB,然后根据三角形的面积公式列式计算即可得解;
②过Q作QF⊥AC交AC延长线于F,利用“角角边”证明△QCF和△PAE全等,根据全等三角形对应边相等可得AE=CF,EP=QF,从而得出AC=EF,再利用“角角边”证明△EPD和△FQD全等,根据全等三角形对应边相等可得DE=DF,从而得解.
(2)①设AP=CQ=x,表示出PB,然后根据三角形的面积公式列式计算即可得解;
②过Q作QF⊥AC交AC延长线于F,利用“角角边”证明△QCF和△PAE全等,根据全等三角形对应边相等可得AE=CF,EP=QF,从而得出AC=EF,再利用“角角边”证明△EPD和△FQD全等,根据全等三角形对应边相等可得DE=DF,从而得解.
解答:(1)解:∵∠B=90°,AB=BC,
∴∠A=∠C=45°,
∵PF∥BC,
∴∠AFP=∠C=45°,
∴△APF是等腰直角三角形,
故答案为:不变,等腰直角三角形;
(2)①解:设AP=CQ=x,则BP=2-x,
∵S△PCQ=
S△ABC,
∴
x(2-x)=
×(
×2×2),
整理得,x2-2x+1=0,
解得x=1,
∴AP=1;
②答:DE的长度不改变,是个定值.
证明:如图,过Q作QF⊥AC交AC延长线于F,
则∠QCF=∠ACB=∠A=45°,
∵PE⊥AC,
∴∠AEP=90°,
∴∠AEP=∠F=90°,
∵点P、Q的速度相等,
∴AP=CQ,
在△QCF和△PAE中,
,
∴△QCF≌△PAE(AAS),
∴AE=CF,EP=QF,
∴AC=AE+EC=CF+EC=EF,
在△EPD和△FQD中,
,
∴△EPD≌△FQD(AAS),
∴DE=DF,
∴DE=
EF=
AC,
∵∠B=90°,AB=BC=2,
∴AC=
=
=2
,
∴DE=
×2
=
是定值.
∴∠A=∠C=45°,
∵PF∥BC,
∴∠AFP=∠C=45°,
∴△APF是等腰直角三角形,
故答案为:不变,等腰直角三角形;
(2)①解:设AP=CQ=x,则BP=2-x,
∵S△PCQ=
| 1 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
整理得,x2-2x+1=0,
解得x=1,
∴AP=1;
②答:DE的长度不改变,是个定值.

证明:如图,过Q作QF⊥AC交AC延长线于F,
则∠QCF=∠ACB=∠A=45°,
∵PE⊥AC,
∴∠AEP=90°,
∴∠AEP=∠F=90°,
∵点P、Q的速度相等,
∴AP=CQ,
在△QCF和△PAE中,
|
∴△QCF≌△PAE(AAS),
∴AE=CF,EP=QF,
∴AC=AE+EC=CF+EC=EF,
在△EPD和△FQD中,
|
∴△EPD≌△FQD(AAS),
∴DE=DF,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠B=90°,AB=BC=2,
∴AC=
| AB2+BC2 |
| 22+22 |
| 2 |
∴DE=
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质与判定,三角形的面积,难点在于(2)②作辅助线构造出全等三角形并二次证明三角形全等.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 明理由.
明理由.
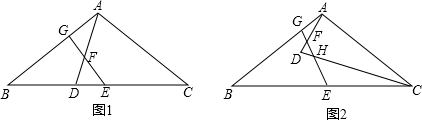
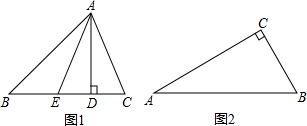 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=