题目内容
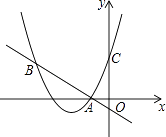
【题目】如图所示,在平面直角坐标系中,过点A(﹣ ![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵x2﹣2x﹣3=0,
∴x=3或x=﹣1,
∴B(0,3),C(0,﹣1),
∴BC=4,
(2)
解:∵A(﹣ ![]() ,0),B(0,3),C(0,﹣1),
,0),B(0,3),C(0,﹣1),
∴OA= ![]() ,OB=3,OC=1,
,OB=3,OC=1,
∴OA2=OBOC,
∵∠AOC=∠BOA=90°,
∴△AOC∽△BOA,
∴∠CAO=∠ABO,
∴∠CAO+∠BAO=∠ABO+∠BAO=90°,
∴∠BAC=90°,
∴AC⊥AB;
(3)
解:设直线AC的解析式为y=kx+b,
把A(﹣ ![]() ,0)和C(0,﹣1)代入y=kx+b,
,0)和C(0,﹣1)代入y=kx+b,
∴ ![]() ,
,
解得:  ,
,
∴直线AC的解析式为:y=﹣ ![]() x﹣1,
x﹣1,
∵DB=DC,
∴点D在线段BC的垂直平分线上,
∴D的纵坐标为1,
∴把y=1代入y=﹣ ![]() x﹣1,
x﹣1,
∴x=﹣2 ![]() ,
,
∴D的坐标为(﹣2 ![]() ,1),
,1),
(4)
解:设直线BD的解析式为:y=mx+n,直线BD与x轴交于点E,
把B(0,3)和D(﹣2 ![]() ,1)代入y=mx+n,
,1)代入y=mx+n,
∴ ![]() ,
,
解得  ,
,
∴直线BD的解析式为:y= ![]() x+3,
x+3,
令y=0代入y= ![]() x+3,
x+3,
∴x=﹣3 ![]() ,
,
∴E(﹣3 ![]() ,0),
,0),
∴OE=3 ![]() ,
,
∴tan∠BEC= ![]() =
= ![]() ,
,
∴∠BEO=30°,
同理可求得:∠ABO=30°,
∴∠ABE=30°,
当PA=AB时,如图1,

此时,∠BEA=∠ABE=30°,
∴EA=AB,
∴P与E重合,
∴P的坐标为(﹣3 ![]() ,0),
,0),
当PA=PB时,如图2,

此时,∠PAB=∠PBA=30°,
∵∠ABE=∠ABO=30°,
∴∠PAB=∠ABO,
∴PA∥BC,
∴∠PAO=90°,
∴点P的横坐标为﹣ ![]() ,
,
令x=﹣ ![]() 代入y=
代入y= ![]() x+3,
x+3,
∴y=2,
∴P(﹣ ![]() ,2),
,2),
当PB=AB时,如图3,

∴由勾股定理可求得:AB=2 ![]() ,EB=6,
,EB=6,
若点P在y轴左侧时,记此时点P为P1,
过点P1作P1F⊥x轴于点F,
∴P1B=AB=2 ![]() ,
,
∴EP1=6﹣2 ![]() ,
,
∴sin∠BEO= ![]() ,
,
∴FP1=3﹣ ![]() ,
,
令y=3﹣ ![]() 代入y=
代入y= ![]() x+3,
x+3,
∴x=﹣3,
∴P1(﹣3,3﹣ ![]() ),
),
若点P在y轴的右侧时,记此时点P为P2,
过点P2作P2G⊥x轴于点G,
∴P2B=AB=2 ![]() ,
,
∴EP2=6+2 ![]() ,
,
∴sin∠BEO= ![]() ,
,
∴GP2=3+ ![]() ,
,
令y=3+ ![]() 代入y=
代入y= ![]() x+3,
x+3,
∴x=3,
∴P2(3,3+ ![]() ),
),
综上所述,当A、B、P三点为顶点的三角形是等腰三角形时,点P的坐标为(﹣3 ![]() ,0),(﹣
,0),(﹣ ![]() ,2),(﹣3,3﹣
,2),(﹣3,3﹣ ![]() ),(3,3+
),(3,3+ ![]() ).
).
【解析】本题考查二次函数的综合问题,涉及一元二次方程的解法,相似三角形的判定,等腰三角形的性质,垂直平分线的判定等知识,内容较为综合,需要学生灵活运用所知识解决.(1)解出方程后,即可求出B、C两点的坐标,即可求出BC的长度;(2)由A、B、C三点坐标可知OA2=OCOB,所以可证明△AOC∽△BOA,利用对应角相等即可求出∠CAB=90°;(3)容易求得直线AC的解析式,由DB=DC可知,点D在BC的垂直平分线上,所以D的纵坐标为1,将其代入直线AC的解析式即可求出D的坐标;(4)A、B、P三点为顶点的三角形是等腰三角形,可分为以下三种情况:①AB=AP;②AB=BP;③AP=BP;然后分别求出P的坐标即可.
【考点精析】掌握因式分解法和线段垂直平分线的判定是解答本题的根本,需要知道已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.