题目内容
如图，在△ABC中，AB=AC，AC是⊙O的弦，BC交⊙O于点D，作∠BAC的外角平分线AE交⊙O于点E，连接DE．求证：DE=AB．
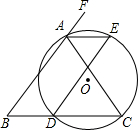
证明：∵AB=AC，
∴∠B=∠C，
∴∠FAC=∠B+∠C=2∠B，
∵AE平分∠FAC，
∴∠FAC=2∠FAE=2∠EAC，
∴∠FAE=∠B，
∴AE∥BC，
∴∠E=∠EDC，
∵∠E=∠C=∠B，
∴ED∥AB，
∵AE∥BC，
∴四边形ABDE是平行四边形，
∴DE=AB．
∴∠B=∠C，
∴∠FAC=∠B+∠C=2∠B，
∵AE平分∠FAC，
∴∠FAC=2∠FAE=2∠EAC，
∴∠FAE=∠B，
∴AE∥BC，
∴∠E=∠EDC，
∵∠E=∠C=∠B，
∴ED∥AB，
∵AE∥BC，
∴四边形ABDE是平行四边形，
∴DE=AB．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
