题目内容
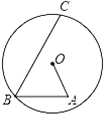
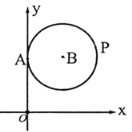
【题目】平面直角坐标系内一点M(x,y)(x≠0),若![]() 则称k为点M的“倾斜比”,如图,⊙B与y轴相切于点A,点B的坐标为(3,5),点P为⊙B上的动点,则点P的“倾斜比”k的最小值是( )
则称k为点M的“倾斜比”,如图,⊙B与y轴相切于点A,点B的坐标为(3,5),点P为⊙B上的动点,则点P的“倾斜比”k的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
作PH⊥x轴于H,如图,设P(x,y),利用性对于得到点P的“倾斜比”k=tan∠POH,则点OP与⊙B相切于P点时,∠POH最小,点P的“倾斜比”k有最小值,连接BP、BA,作BD⊥x轴于D,交OP于C,如图,根据切线的性质得到BA⊥y轴,BP⊥OP,BA=BP=3,证明△OCD≌△BCP得到BC=OC,设CD=t,则BC=OC=5-t,利用勾股定理得到22+t2=(5-t)2,解方程求出t得到tan∠POH=![]() ,从而得到点P的“倾斜比”k的最小值.
,从而得到点P的“倾斜比”k的最小值.
解:作PH⊥x轴于H,如图,
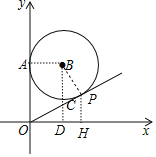
设P(x,y),
∵点P的“倾斜比”![]() =tan∠POH,
=tan∠POH,
∴当点P的“倾斜比”k取最小值时,∠POH最小,
∴点OP与⊙B相切于P点时,∠POH最小,点P的“倾斜比”k有最小值,
连接BP、BA,作BD⊥x轴于D,交OP于C,如图,
∵⊙B与y轴相切于点A,OP切⊙B于P,点B的坐标为(3,5),
∴BA⊥y轴,BP⊥OP,BA=BP=3,
∴OD=3,
在△OCD和△BCP中
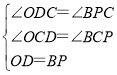
∴△OCD≌△BCP(AAS),
∴BC=OC,
设CD=t,则BC=OC=5-t,
在Rt△OCD中,22+t2=(5-t)2,解得t=![]() ,
,
即CD=![]() ,
,
∴tan∠POH=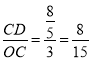 ,
,
即点P的“倾斜比”k的最小值是![]() .
.
故选:D.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目