Question

【题目】已知抛物线C：y=-x2+bx+c经过A（-3，0）和B（0，3）两点，将这条抛物线的顶点记为M，它的对称轴与x轴的交点记为N．

（1）求抛物线C的表达式；

（2）求点M的坐标；

（3）将抛物线C平移到抛物线C′，抛物线C′的顶点记为M′，它的对称轴与x轴的交点记为N′．如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形，那么应将抛物线C怎样平移？为什么？

Answer 1

【答案】（1）y=-x2-2x+3；（2）M（-1，4）．（3）将抛物线C向左或向右平移4个单位可得符合条件的抛物线C′或将抛物线C先向左或向右平移4个单位，再向下平移8个单位，可得符合条件的抛物线C′．理由见解析.

【解析】

（1）直接把A（-3，0）和B（0，3）两点代入抛物线y=-x2+bx+c，求出b，c的值即可；

（2）根据（1）中抛物线的解析式可得出其顶点坐标；

（3）根据平行四边形的定义，可知有四种情形符合条件，如解答图所示．需要分类讨论．

解：（1）∵抛物线y=-x2+bx+c经过A（-3，0）和B（0，3）两点，

∴，

解得，

故此抛物线的解析式为：y=-x2-2x+3；

（2）∵由（1）知抛物线的解析式为：y=-x2-2x+3，

∴当x=-时，y=4，

∴M（-1，4）．

（3）由题意，以点M、N、M′、N′为顶点的平行四边形的边MN的对边只能是M′N′，

∴MN∥M′N′且MN=M′N′．

∴MNNN′=16，

∴NN′=4．

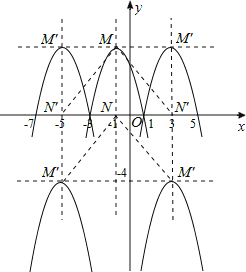
i）当M、N、M′、N′为顶点的平行四边形是MNN′M′时，将抛物线C向左或向右平移4个单位可得符合条件的抛物线C′；

ii）当M、N、M′、N′为顶点的平行四边形是MNM′N′时，将抛物线C先向左或向右平移4个单位，再向下平移8个单位，可得符合条件的抛物线C′．

∴上述的四种平移，均可得到符合条件的抛物线C′．