题目内容
【题目】已知抛物线y=x2+bx+c的对称轴l交x轴于点A.
(1)若此抛物线经过点(1,2),当点A的坐标为(2,0)时,求此抛物线的解析式;
(2)抛物线y=x2+bx+c交y轴于点B,将该抛物线平移,使其经过点A,B,且与x轴交于另一点C.若b2=2c,b≤﹣1,比较线段OB与OC+![]() 的大小.
的大小.
【答案】(1)y=x2﹣4x+5;(2)当﹣3<b≤﹣1时,OB<OC+![]() ;当b=﹣3时,OB=OC+
;当b=﹣3时,OB=OC+![]() ;当b<﹣3时,OB>OC+
;当b<﹣3时,OB>OC+![]() .
.
【解析】
(1)根据抛物线y=x2+bx+c经过点(1,2),对称轴l交x轴于点A(2,0),列出关于b、c的方程组,解方程组即可求得此抛物线的解析式;
(2)先求出点A(﹣![]() ,0),B(0,
,0),B(0,![]() ),然后设平移后的抛物线的解析式为y=(x+
),然后设平移后的抛物线的解析式为y=(x+![]() +h)2+
+h)2+![]() +k,代入A、B的坐标,求得
+k,代入A、B的坐标,求得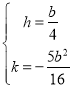 ,那么平移后的抛物线的解析式为y=(x+
,那么平移后的抛物线的解析式为y=(x+![]() +
+![]() )2+
)2+![]() ﹣
﹣![]() =x2+
=x2+![]() bx+
bx+![]() b2,然后求得C的坐标,得出OB=
b2,然后求得C的坐标,得出OB=![]() ,OC=﹣b,OC+
,OC=﹣b,OC+![]() =﹣b+
=﹣b+![]() ,即可判断OB与OC+
,即可判断OB与OC+![]() 的大小.
的大小.
解:(1)根据题意,得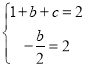 ,
,
解得![]() ,
,
所以此抛物线的解析式为y=x2﹣4x+5;
(2)∵抛物线y=x2+bx+c交y轴于点B,对称轴l交x轴于点A,
∴B(0,c),A(﹣![]() ,0),
,0),
∵b2=2c,
∴c=![]() ,
,
∴y=x2+bx+c=x2+bx+![]() =(x+
=(x+![]() )2+
)2+![]() ,
,
设平移后的抛物线的解析式为y=(x+![]() +h)2+
+h)2+![]() +k,
+k,
∵抛物线经过点A(﹣![]() ,0),B(0,
,0),B(0,![]() ),
),
∴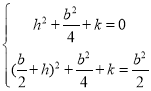 ,解得
,解得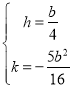 ,
,
∴平移后的抛物线的解析式为y=(x+![]() +
+![]() )2+
)2+![]() ﹣
﹣![]() =x2+
=x2+![]() bx+
bx+![]() b2,
b2,
令y=0,则x2+![]() bx+
bx+![]() b2=0,
b2=0,
解得x1=﹣![]() ,x2=﹣b,
,x2=﹣b,
∴C(﹣b,0),
∴OB=![]() ,OC=﹣b,
,OC=﹣b,
∴OC+![]() =﹣b+
=﹣b+![]() ,
,
∵OB﹣(OC+![]() )=
)=![]() ﹣(﹣b+
﹣(﹣b+![]() )=
)=![]() +b﹣
+b﹣![]() =
=![]() (b2+2b﹣3)=
(b2+2b﹣3)=![]() (b+3)(b﹣1),
(b+3)(b﹣1),
而b≤﹣1,
∴当﹣3<b≤﹣1时,OB<OC+![]() ;
;
当b=﹣3时,OB=OC+![]() ;
;
当b<﹣3时,OB>OC+![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案