��Ŀ����
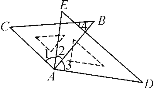
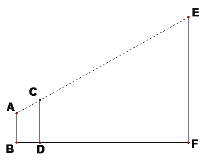
����Ŀ����ͼ��ij������ҵ�ֵ���ڣ���ѧ������ȤС���ͬѧ����������ѧ��֪ʶ��������֧�ܵ���ߵ�E������ľ���EF����������֧�ܵ�����BC����洹ֱ������BCA=90�㣬��BC=1.5m����F��A��C��ͬһ��ˮƽ���ϣ�б��AB��ˮƽ��AC�ļнǡ�BAC=30�㣬֧�Ÿ�DE��AB�ڵ�D����֧�ܵı�BE��AB�ļнǡ�EBD=60�㣬�ֲ��AD=1m�����������֧�ܵı�BE������E������ľ���EF�ij��ȣ�
���𰸡��⣺��B��BH��EF�ڵ�H��

���ı���BCFHΪ���Σ�BC=HF=1.5m����HBA=��BAC=30�㣬
��Rt��ABC��
�ߡ�BAC=30�㣬BC=1.5m��
��AB=3m��
��AD=1m��
��BD=2m��
��Rt��EDB��
�ߡ�EBD=60�㣬
���BED=90�㩁60��=30�㣬
��EB=2BD=2��2=4m��
�֡ߡ�HBA=��BAC=30�㣬
���EBH=��EBD����HBD=30�㣬
��EH= ![]() EB=2m��
EB=2m��
��EF=EH+HF=2+1.5=3.5��m����
�𣺸�֧�ܵı�BEΪ4m������E������ľ���EF�ij���Ϊ3.5m��
����������ֱ����������30�����Ե�ֱ�DZߵ���б�ߵ�һ��ɵ����ڡ�BAC=30�㣬BC=1.5m������AB=3m���Ӷ�AD=1m��BD=2m������������ֱ����������30�����Ե�ֱ�DZߵ���б�ߵ�һ���������EB=2BD=2��2=4m��
�ڼ��㶥��E������ľ���EF�ij���ʱ�����ǿ����������߰�EF��ΪEH��HF�����֣�����HF����BC����1.5m����EH��Ȼ����ֱ����������30�����Ե�ֱ�DZߵ���б�ߵ�һ����EH=![]() EB=2m�����õ�EF�ij���Ϊ3.5m
EB=2m�����õ�EF�ij���Ϊ3.5m

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�