题目内容
【题目】如图,在平面直角坐标系中,已知矩形![]() 的顶点
的顶点![]() ,动点
,动点![]() ,
,![]() 同时从
同时从![]() 点出发,点
点出发,点![]() 沿射线
沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度运动,点
个单位的速度运动,点![]() 沿线段
沿线段![]() 方向以每秒
方向以每秒![]() 个单位的速度运动,当点
个单位的速度运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() ,
,![]() 同时停止运动,连接
同时停止运动,连接![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).
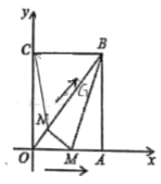
(1)求证![]() ;
;
(2)当点![]() 运动到点
运动到点![]() 时,若双曲线
时,若双曲线![]() 的图象恰好过点
的图象恰好过点![]() ,试求
,试求![]() 的值;
的值;
(3)连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
【答案】(1)证明见解析;(2)k=4.32;(3) ∴当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时
时![]() 为等腰三角形.
为等腰三角形.
【解析】
(1)只需证明![]() ,即可完成证明;
,即可完成证明;
(2)先确定ON的长度,再确定点N的坐标,再利用待定系数法求解即可;
(3)分当NB=CB或CN=BN或CN=BC分类讨论解答即可;
(1)证明:由题意:OA=6,AB=8,BC=6,OB=10,OM=t,ON=0.6t,
∴![]()
又∵∠MON=∠AOB,
∴△ONM∽△OAB.
(2)当点![]() 运动到点
运动到点![]() 时,即OM=5时,ON=0.6t=3
时,即OM=5时,ON=0.6t=3
过N作NF⊥y轴,NE⊥x轴,设N点坐标为(m,n)
∴sin∠COB=![]()
∴FN=1.8
同理:NE=2.4
∴N点坐标为(1.8,2.4)
∵双曲线![]() 的图象恰好过点
的图象恰好过点![]()
∴k=2.4×1.8=4.32
(3)①当NB=CB时,即10-0.6t=6,解得t= ![]() 时,
时, ![]() 为等腰三角形.
为等腰三角形.
②当CN=BN时,即N在CB的垂直平分线上,
∴N为OB的中点
∴ON=5=0.6t
∴t=![]()
③当CN=BC=6时,设N点坐标为(3a,4a),则ON=5a=0.6t
∴![]() 即
即![]() ,解得a=2或a=
,解得a=2或a=![]()
当a=2时,ON=10,N点和B点重合,不能构成三角形,舍去;
当a=![]() 时, ON=5a=2.8=0.6t,解得t=
时, ON=5a=2.8=0.6t,解得t=![]()
∴当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时
时![]() 为等腰三角形.
为等腰三角形.

【题目】舍利生生塔位于晋祠南瑞,建于隋开皇年间,宋代重修,清乾隆十六年(1751年)重建.七屋八角,琉璃瓦顶,远远望去,高耸的古塔,映衬着蓝天白云,甚是壮观.原塔内每层均有佛像,开4门8窗,凭窗远眺,晋祠内外美景可一览无余.如果在夕阳西下时欣赏宝塔,还会出现——天云锦、满塔光辉的壮丽景观,被誉为“宝塔披霞”.某数学“综合与实践”小组的同学把“测量舍利生生塔高”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量,测量结果如表:
课题 | 测量舍利生生塔高 | |||
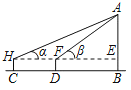
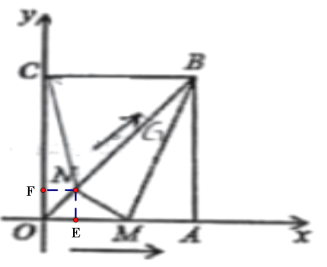
测量示意图 |
| 说明:某同学在地面上选择点C,使用手持测角仪,测得此时楼顶A的仰角∠AHE=α,沿CB方向前进到点D,测量出C,D之间的距离CD=xm,在点D使用手持测角仪,测得此时楼顶A的仰角∠AFE=β | ||
测量数据 | α的度数 | β的度数 | CD的长度 | 该同学眼睛离地面的距离HC |
24° | 37° | 32m | 1.76m | |
… | … | |||
(1)请帮助该小组的同学根据上表中的测量数据,求塔高AB.(结果精确到1m;参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(2)该小组要写出一份完整的课题活动报告,除上表中的项目外,你认为还需要补充哪些项目?(写出一个即可)