题目内容
【题目】如图,在![]() 中,
中,![]() 于D,且
于D,且![]() ,以AB为底边作等腰直角三角形ABE,连接ED、EC,延长CE交AD于点F,下列结论:①
,以AB为底边作等腰直角三角形ABE,连接ED、EC,延长CE交AD于点F,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的有( ).
,其中正确的有( ).

A.①②B.①③C.①②③D.①②③④
【答案】D
【解析】
①易证∠CBE=∠DAE,用SAS即可求证:△ADE≌△BCE;②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;③证明△AEF≌△BED即可;④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
解:∵AD为△ABC的高线
∴∠CBE+∠ABE+∠BAD=90°,
∵Rt△ABE是等腰直角三角形,
∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,
∴∠CBE+∠BAD=45°,
∴∠DAE=∠CBE,
在△DAE和△CBE中,
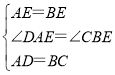
∴△ADE≌△BCE(SAS);
故①正确;
∵△ADE≌△BCE,
∴∠EDA=∠ECB,AD=BC,DE=EC,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠ECB=90°,
∴∠DEC=90°,
∴CE⊥DE,△DEC是等腰直角三角形,易证△DFC是等腰直角三角形,
故③正确,
∴DF=DC,
∵BC=BD+DC=BD+DF=AD,
故②正确;
∵AD=BC,BD=AF,
∴CD=DF,
∵AD⊥BC,
∴△FDC是等腰直角三角形,
∵DE⊥CE,
∴EF=CE,
∴S△AEF=S△ACE,
∵△AEF≌△BED,
∴S△AEF=S△BED,
∴S△BDE=S△ACE.
故④正确;
故选:D.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:
频数分布表:
组别 | 跳绳(次/1分钟) | 频数 |
第1组 | 190~199 | 5 |
第2组 | 180~189 | 11 |
第3组 | 170~179 | 23 |
第4组 | 160~169 | 33 |
请回答下列问题:
(1)此次测试成绩的中位数落在第 组中;
(2)如果成绩达到或超过180次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的 %;
(3)如果该校九年级参加体育测试的总人数为200人,若要绘制一张统计该校各项目选考人数分布的扇形图(如图),图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比,那么该扇形的圆心角应为 °;
(4)如果此次测试的平均成绩为171次/分钟,那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平?为什么?





