��Ŀ����
����Ŀ��ijУΪ�˽���꼶ѧ��һѧ�ڲμӹ�����ʱ���������ȡ50�����꼶ѧ��Ϊ�������е��飬���μӹ�����ʱ��t����λ��Сʱ�����������ֳ����ࣺA�ࣨ0��t��2����B�ࣨ2��t��4����C�ࣨ4��t��6����D�ࣨ6��t��8����E�ࣨt��8�������Ƴ��в�����������ͳ��ͼ��
��1�������У�E��ѧ������ ���ˣ��벹ȫ����ͳ��ͼ��
��2����У���꼶��600��ѧ��������꼶�μӹ���ʱ��6��t��8��ѧ������
��3����������ѡȡ�μӹ���ʱ����0��t��4��2����־Ը�ߣ�����2�˲μӹ���ʱ�䶼��2��t��4�еĸ��ʣ�

���𰸡���1��5��2��216��3��![]()
��������
��1��E��ѧ��������50����2+3+22+18������2������D��ѧ������ռ�������������İٷֱȣ��ٹ���������������꼶�μӹ���ʱ��6��t��8��ѧ����Ϊ600��36%����3�����оٷ��������п���������ٸ��ݸ��ʹ�ʽ�����2�����幤ʱ�䶼��2��t��4�еĸ���.
�⣺��1��E��ѧ����50����2+3+22+18��=5���ˣ���
��ȫͼ�����£�
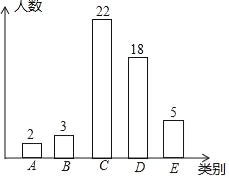
�ʴ�Ϊ��5��
��2��D��ѧ������ռ��������������![]() ��100%=36%��
��100%=36%��
�����꼶�μӹ���ʱ��6��t��8��ѧ����Ϊ600��36%=216���ˣ���
��3����0��t��2�ڵ�����Ϊ�ס��ң�2��t��4�ڵ�3�˼�ΪA��B��C��
������ѡ�����У����ҡ���A����B����C����A����B����C��AB��AC��BC��10�ֿ��ܽ����
����2�����幤ʱ�䶼��2��t��4�е���AB��AC��BC��3�ֽ����
����2�����幤ʱ�䶼��2��t��4�еĸ���Ϊ![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�