��Ŀ����
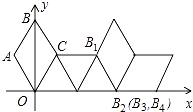
����Ŀ���������ֱ�����ǰ��ABC�͡�DEC��ͼ�ڷţ����С�ACB=��DCE=90��F��DE���е㣬H��AE���е㣬G��BD���е㣮
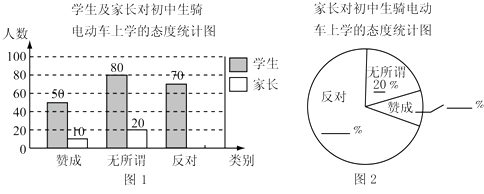
��1����ͼ1������D��E�ֱ���AC��BC���ӳ����ϣ�ͨ���۲�Ͳ���������FH��FG��������ϵΪ��λ�ù�ϵΪ��
��2����ͼ1�����ǰ��DEC���ŵ�C˳ʱ�루��ʱ�룩��ת����ת��Ϊa��0�㣼a��180�㣩��ͼ2��ͼ3�����Ϊ��������ͼ2����ת����A��C��E��һ��ֱ����ʱ���������������䣬��1���еIJ����Ƿ�����������������˵�����ɣ������������ͼ2��ͼ3��ѡ��һ֤��
��3���ڡ�DEC�Ƶ�C��ͼ3��ʽ��ת�Ĺ����У���ֱ��FH������Cʱ����AC=2��CD= ![]() ����ֱ��д��FG�ij���
����ֱ��д��FG�ij���
���𰸡�
��1��FG=FH��FG��FH
��2��
�ٴ𣺳�����
֤������ͼ2�У�
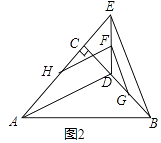
��CE=CD����ECD=��ACD=90�㣬AC=BC��
���ACD�ա�BCE
��AD=BE��
�ɣ�1��֪��FH= ![]() AD��FH��AD��FG=
AD��FH��AD��FG= ![]() BE��FG��BE��
BE��FG��BE��
��FH=FG��FH��FG��
�ࣨ1���еIJ��뻹������
�ڴ𣺳�����������FH=FG��FH��FG��
��ͼ3�У�����AD��BE�����߽���Z��AD��BC��X��
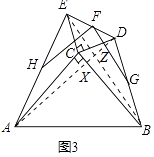
ͬ��1����֤
��FH= ![]() AD��FH��AD��FG=
AD��FH��AD��FG= ![]() BE��FG��BE��
BE��FG��BE��
��������ECD��ACB�ǵ���ֱ�������Σ�
��CE=CD��AC=BC����ECD=��ACB=90�㣬
���ACD=��BCE��
�ڡ�ACD�͡�BCE��
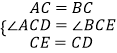 ��
��
���ACD�ա�BCE��
��AD=BE����EBC=��DAC��
�ߡ�DAC+��CXA=90�㣬��CXA=��DXB��
���DXB+��EBC=90�㣬
���EZA=180�㩁90��=90�㣬
��AD��BE��
��FH��AD��FG��BE��
��FH��FG��
��FH=FG��FH��FG��
������FH=FG��FH��FG��
��3��
��ͼ4�У�
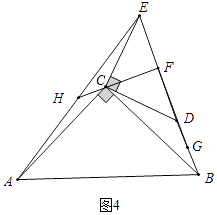
�����⣬��֪CF��DE����CFD����CFE���ǵ���ֱ�������Σ�
��CD= ![]() ��
��
��CF=DF=1����BC=AC=2��
��BF= ![]() =
= ![]() ��
��
��BD=BF��DF= ![]() ��1��
��1��
��DG=GB��
��DG= ![]() ��
�� ![]() ��1����
��1����
��FG=DF+DG= ![]() ��
��
����������1���⣺��ͼ1�У�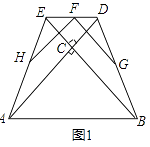
��CE=CD��AC=BC����ECA=��DCB=90�㣬
��BE=AD��
��F��DE���е㣬H��AE���е㣬G��BD���е㣬
��FH= ![]() AD��FH��AD��FG=
AD��FH��AD��FG= ![]() BE��FG��BE��
BE��FG��BE��
��FH=FG��
��AD��BE��
��FH��FG��
���Դ��ǣ�FG=FH��FG��FH��
�����㾫�����������⣬������Ҫ�˽����ֱ��������(����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45��)����Ҫ������ת������(����ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ���)�����֪ʶ���Ǵ���Ĺؼ���

 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д�����Ŀ��ijˮ�����������ڣ������Ϊ10Ԫ/���ij��ˮ�����������ν��ۺ�ļ۸�Ϊ8.1Ԫ/��������ν��۵İٷ�����ͬ��
��1�������ˮ��ÿ�ν��۵İٷ��ʣ�
��2���ӵ�һ�ν��۵ĵ�1�����𣬵�x�죨xΪ���������ۼۡ��������������ķ��õ������Ϣ�����ʾ����֪����ˮ���Ľ���Ϊ4.1Ԫ/������۸�ˮ����x���죩������Ϊy��Ԫ������y��x��1��x��15��֮��ĺ�����ϵʽ��������ڼ���ʱ�����������
ʱ��x���죩 | 1��x��9 | 9��x��15 | x��15 |
�ۼۣ�Ԫ/� | ��1�ν��ۺ�ļ۸� | ��2�ν��ۺ�ļ۸� | |
������� | 80��3x | 120��x | |
�������ķ��ã�Ԫ�� | 40+3x | 3x2��64x+400 | |
��3���ڣ�2���������£���Ҫʹ��15�������ȣ�2����������������127.5Ԫ�����15���ڵ�14��ļ۸���������ɽ�����Ԫ��