题目内容
【题目】阅读理解:
【问题情境】金老师给“数学小达人”小明和小军提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC.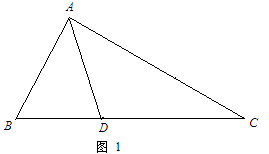
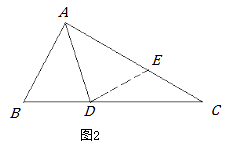
【证明思路】小明的证明思路是:如图2,在AC上截取AE=AB,连接DE.……
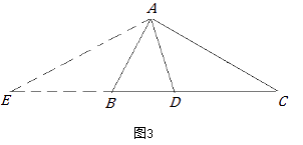
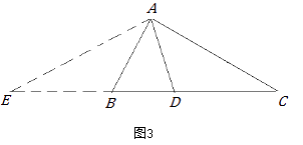
小军的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE.……
(1)请你从他们的思路中,任意选择一种思路继续完成下一步的证明.
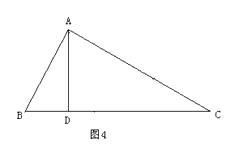
(2)【变式探究】如图4,金老师把“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变,那么AB+BD=AC还成立吗?若成立,请证明;若不成立,写出正确结论,并说明理由.
(3)【迁移拓展】如图5,△ABC中,∠B=2∠C.求证:AC2—AB2=AB×BC.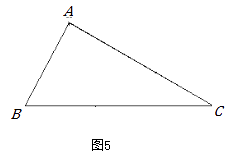
【答案】
(1)解:小明的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
∵AD是∠BAC的平分线,∴∠BAD=∠EAD,
又∵AD=AD, ∴△ABD≌△AED,∴BD=DE,∠ABD=∠AED,
又∵∠AED=∠EDC+∠C,∠B=2∠C,
∴∠EDC=∠C,∴ DE=EC, 即AB+BD=AC.
小军的证明思路是:延长CB至点E,使BE=AB,连接AE.(如图3)
则∠E=∠BAE,∴∠ABC=2∠E,
∵∠ABC=2∠C,∴∠E=∠C,∴△AEC是等腰三角形.
∵∠ADE=∠DAC+∠C,∠DAE=∠BAD+∠BAE,
又∵AD是∠BAC的平分线, ∴∠BAD=∠DAC,
∴∠ADE=∠DAE,∴△AED是等腰三角形.
∴EA=ED=AC,∴AB+BD=AC.
(2)解:AB+BD=AC不成立.正确结论是:AB+BD=CD.
方法1:如图4,在CD上截取DE=DB,
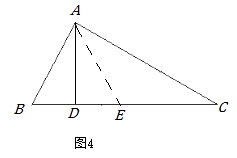
∵AD⊥BC, ∴ AD是BE的垂直平分线,
∴AE=AB, ∴∠B=∠AED,
∵∠AED =∠C+∠CAE,
∵∠B=2∠C,∴∠C=∠CAE,
∴ AE=EC, 即AB+BD=CD.
方法2:如图5,延长DB至点E,使BE=AB,则∠E=∠BAE,
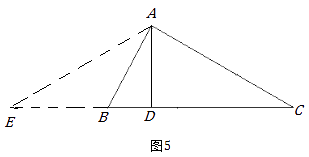
∵∠ABD =∠E+∠BAE =2∠E,
∵∠B=2∠C,∴∠E=∠C,∴△AEC是等腰三角形.
∵AD⊥BC,∴CD=ED, 即AB+BD=CD.
(3)解:如图6,过点A作AD⊥BC于D.
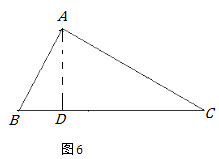
由勾股定理得:AB2=BD2+AD2, AC2=CD2+AD2,
∴ AC2—AB2=CD2—BD2=(CD+BD)×(CD—BD)=BC×(CD—BD),
∵AB+BD=CD,∴ CD—BD=AB,
∴ AC2—AB2=BC×(CD—BD)=BC×AB,即AC2-AB2+AB×BC.
【解析】(1)根据已知条件和角平分线的性质,得到△ABD≌△AED,根据根据三角形的一个外角等于和它不相邻的两个内角的和和∠B=2∠C,得到∠EDC=∠C,根据等角对等边得到DE=EC, 即AB+BD=AC;(2)根据已知条件由AD⊥BC,得到AD是BE的垂直平分线,根据垂直平分线得到AB+BD=CD;(3)根据勾股定理和两等式相减,得到AC2-AB2+AB×BC.

 阅读快车系列答案
阅读快车系列答案