Question

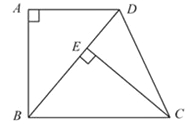
【题目】如图，点P是等边△ABC内一点，PA=6，PB=8，PC=10，则△APC的面积是__________

Answer 1

【答案】

【解析】把△APC绕点A顺时针旋转60°，使点P旋转到点D，连接PD；作BE⊥AP交AP的延长线与点E.

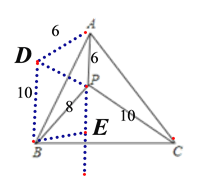
由旋转的性质得，

AD=AP=6,BD=PC=10，∠DAP=60°,

∴△ADP是等边三角形，

∴∠APD=60°,DP=AP=6.

∵62+82=102，

∴DP2+BP2=BD2，

∴△BPD是直角三角形，

∴∠BPD=90°,

∴∠APB=90°+60°=150°,

∴∠BPE=180°-150°=30°,

∴BE=BP÷2=8÷2=4.

S△APC=S△ABD=S四边形ADBP-S△ABP

= S△APD+S△BPD -S△ABP

=

.