题目内容
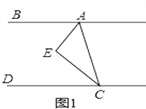
【题目】如图，抛物线 
与x轴交于两点A（﹣4，0）和B（1，0），与y轴交于点C（0，2），动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动，过点D作x轴的垂线，交△ABC的另一边于点E，将△ADE沿DE折叠，使点A落在点F处，设点D的运动时间为t秒．
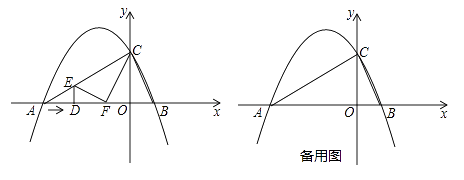
（1）求抛物线的解析式和对称轴；
（2）是否存在某一时刻t，使得△EFC为直角三角形？若存在，求出t的值；若不存在，请说明理由；
（3）设四边形DECO的面积为s，求s关于t的函数表达式．
【答案】
（1）解：把A（﹣4，0），B（1，0），点C（0，2）代入 
得： 
，解得： 
，
∴抛物线的解析式为： 
，
对称轴为：直线x=﹣ 
；
（2）解：存在，∵AD=2t，
∴DF=AD=2t，
∴OF=4﹣4t，
∴D（2t﹣4，0），
∵直线AC的解析式为： 
，∴E（2t﹣4，t），
∵△EFC为直角三角形，分三种情况讨论：
① 当∠EFC=90°，则△DEF∽△OFC，
∴ 
，即 
，解得：t= 
；
②当∠FEC=90°，
∴∠AEF=90°，
∴△AEF是等腰直角三角形，
∴DE= 
AF，即t=2t，
∴t=0，（舍去），
③当∠ACF=90°，则AC2+CF2=AF2 ， 即（42+22）+[22+（4t﹣4）2]=（4t）2 ， 解得：t= 
，
∴存在某一时刻t，使得△EFC为直角三角形，此时，t= 或 ；
（3）解：∵B（1，0），C（0，2），
∴直线BC的解析式为：y=﹣2x+2，
当D在y轴的左侧时，S= （DE+OC）OD= （t+2）（4﹣2t）=﹣t2+4 （0＜t＜2）；
当D在y轴的右侧时，如图2，
∵OD=4t﹣4，DE=﹣8t+10，S= （DE+OC）OD= （﹣8t+10+2）（4t﹣4），即 
（2＜t＜ 
）．
综上所述： 
【解析】（1）（1）利用待定系数法，将点A、B、C的坐标代入函数解析式，建立方程组求解即可。
（2）根据题意分别求出AD、DF、OF的长，表示出点D的坐标，利用待定系数法求出直线BC的函数解析式，表示出点E的坐标，再分三种情况讨论△EFC为直角三角形：① 当∠EFC=90°，则△DEF∽△OFC，根据相似三角形的性质，列出关于t的方程求解即可；②∠FEC=90°，∠AEF=90°，△AEF是等腰直角三角形求出t的值即可；③当∠ACF=90°，则AC2+CF2=AF2 ， 建立关于t的方程求解即可，从而可得出答案。
（3）求得直线BC的解析式为：y=-2x+2，当D在y轴的左侧时，当D在y轴的右侧时，如图2，根据梯形的面积公式即可得到结论。
