Question

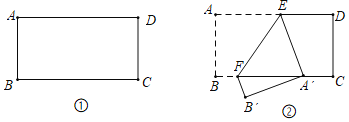
【题目】如图①，在矩形纸片ABCD中，AB=4，AD=6．点E，F分别在AB，DC上（E不与A，D重合，F不与B，C重合），现以EF为折痕，将矩形纸片ABCD折叠．

（1）当A点落在BC上时（如图②），求证：△EFA′是等腰三角形；

（2）当A′点与C重合时，试求△EFA’的面积；

（3）当A′点与DC的中点重合时，试求折痕EF的长．

Answer 1

【答案】（1）见解析；（2）△EFA'的面积；（3）EF=．

【解析】

（1）先判断出AD∥BC，进而得出∠AEF=∠EFA'=∠FEA'，即可得出结论；

（2）先准确画图，设BF=a，则FC=6-a，根据勾股定理计算x的值，表示BF=，FC=6-=，根据三角形面积公式可得结论；

（3）作辅助线，先利用勾股定理计算AA'的长，证明△ADA'∽△FME，列比例式可得EF的长．

（1）如图②，∵四边形ABCD是矩形，

∴AD∥BC，

∴∠AEF=∠EFA'，

由折叠性质可得，∠AEF=∠FEA’，

∴∠FEA'=∠EFA'，

∴A'E=A'F，

∴△EFA′是等腰三角形；

（2）如下图，设BF=a，则FC=6-a，

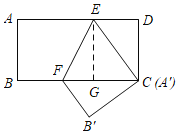
∵CB'=AB=4，

在Rt△FCB'中，由勾股定理得：x2+42=（6-x）2，

x=，

∴BF=，FC=6-=，

过E作EG⊥BC于G，则EG=AB=4，

∴△EFA'的面积===；

（3）过点F作FM⊥AD，连接AA'，

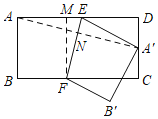
∵AD=6，A'D=CD=2，

∴AA'===2，

由折叠得：∠AEF=∠A'EF，AE=A'E，

∴∠EAA'=∠EA'A，

∴∠ANE=∠A'NE=90°=∠AMF，

∴∠DAA'=∠MFE，

∵∠FME=∠ADA'=90°，

∴△ADA'∽△FME，

∴，

∴，EF=．