题目内容
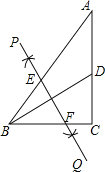
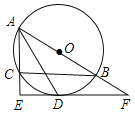
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,由OA=OD知∠OAD=∠ODA,由AD平分∠EAF知∠DAE=∠DAO,据此可得∠DAE=∠ADO,继而知OD∥AE,根据AE⊥EF即可得证;
(2)作OG⊥AE,知AG=CG=![]() AC=2,证四边形ODEG是矩形得OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=48,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
AC=2,证四边形ODEG是矩形得OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=48,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
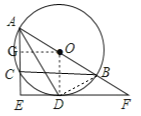
(1)如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠EAF,
∴∠DAE=∠DAO,
∴∠DAE=∠ADO,
∴OD∥AE,
∵AE⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)如图,作OG⊥AE于点G,连接BD,
则AG=CG=![]() AC=2,∠OGE=∠E=∠ODE=90°,
AC=2,∠OGE=∠E=∠ODE=90°,
∴四边形ODEG是矩形,
∴OA=OB=OD=CG+CE=2+2=4,∠DOG=90°,
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD,
∴![]() ,即
,即![]() ,
,
∴AD2=48,
在Rt△ABD中,BD=![]() =4,
=4,
在Rt△ABD中,∵AB=2BD,
∴∠BAD=30°,
∴∠BOD=60°,
则![]() 的长度为
的长度为![]() .
.

【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.