题目内容
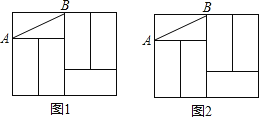
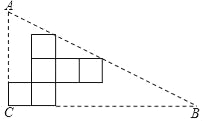
【题目】如图,在Rt△ABC纸片上可按如图所示方式剪出一正方体表面展开图,直角三角形的两直角边与正方体展开图左下角正方形的边共线,斜边恰好经过两个正方形的顶点,已知BC=24cm,则这个展开图可折成的正方体的体积为_____cm3.
【答案】27
【解析】
首先设这个展开图围成的正方体的棱长为xcm,然后延长FE交AC于点D,根据三角函数的性质,可求得AC的长,然后由相似三角形的对应边成比例,即可求得答案.
解:如图,设这个展开图围成的正方体的棱长为xcm,
延长FE交AC于点D,
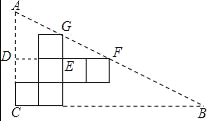
则EF=2xcm,EG=xcm,DF=4xcm,
∵DF∥BC,
∴∠EFG=∠B,
∵在Rt![]() GEF中,tan∠EFG=
GEF中,tan∠EFG=![]() ,
,
∴在Rt![]() ABC中,tanB=
ABC中,tanB=![]() ,
,
∵BC=24cm,
∴AC=12cm,
∴AD=AC﹣CD=12﹣2x(cm)
∵DF∥BC,
∴△ADF∽△ACB,
∴![]() ,
,
即![]() ,
,
解得:x=3,
即这个展开图围成的正方体的棱长为3cm,
∴这个展开图可折成的正方体的体积为27cm3.
故答案为:27.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目