题目内容
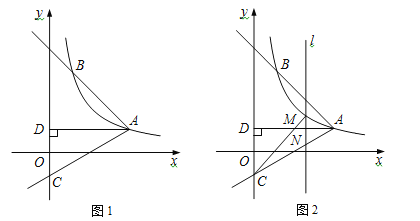
【题目】如图,在四边形![]() 中
中![]() ,
,![]() ,
,![]() ,点
,点![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,连接
处,连接![]() 并延长交射线
并延长交射线![]() 于点
于点![]() .
.
(1)如果![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 在边
在边![]() 上时,连接
上时,连接![]() ,设
,设![]() ,求
,求![]() 关于
关于![]() 的函数关系式并写出
的函数关系式并写出![]() 的取值范围;
的取值范围;
(3)连接![]() ,如果
,如果![]() 是等腰三角形,求
是等腰三角形,求![]() 的长.
的长.
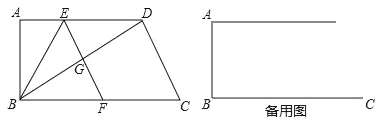
【答案】(1)9;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据翻折的性质可得BG=AB=6,由![]() 可求得BF=9,利用
可求得BF=9,利用![]() ,即可求解;
,即可求解;
(2)过点![]() 作
作![]() 交于点
交于点![]() ,连接
,连接![]() ,设:
,设:![]() ,∠DBC=α,则在
,∠DBC=α,则在![]() 中,
中,![]() ,
,![]() ,
,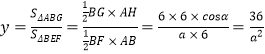 ,
,![]() ,联立即可求解;
,联立即可求解;
(3)分![]() 两种情况,求解即可.
两种情况,求解即可.
解:(1)将![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,
处,
∴![]() ,
,
![]() ,则:
,则:![]() ,
,
![]() ,即:
,即:![]() ,
,
则![]() ;
;
(2)过点![]() 作
作![]() 交于点
交于点![]() ,连接
,连接![]() ,设:
,设:![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,
,
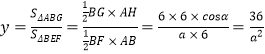 ①
①
![]() ,解得:
,解得:![]() ②
②
把②式代入①式整理得:![]() ;
;
(3)①当![]() 时,
时,
![]() ,
,
把②式代入上式并解得:![]() ,
,
②当![]() 时,
时,
同理可得:![]() ;
;
故:![]() 的长为
的长为![]() 或
或![]() .
.
故答案为:(1)9;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目