题目内容
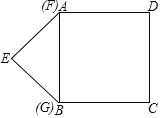
【题目】如图,正方形ABCD中,点E、F、G分别为边AB、BC、AD上的中点,连接AF、DE交于点M,连接GM、CG,CG与DE交于点N,则结论①GM⊥CM;②CD=DM;③四边形AGCF是平行四边形;④∠CMD=∠AGM中正确的有( )个.
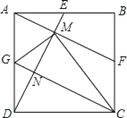
A. 1B. 2C. 3D. 4
【答案】B
【解析】
先根据正方形的性质和中点的性质判断③正确,再根据SAS证出△ADE≌△BAF,得出∠AME=90°,从而证出∠GND=90°再根据直角三角形斜边上的中线等于斜边的一半,得出DG=MG,,利用等腰三角形的三线合一,得出DN=MN,从而得出CG垂直平分DM,从而得出①②正确,再利用等腰三角形的性质和四边形的内角和证明④不成立即可.
解:正方形ABCD中,AD=BC
∵点E、F、分别为边AB、BC上的中点,
∴AG∥FC且AG=FC,
∴四边形AGCF为平行四边形,故③正确;
∴AF//CG
∴∠GAF=∠FCG=∠DGC,∠AMN=∠GND
在△ADE和△BAF中,
∵ ,
,
∴△ADE≌△BAF(SAS),
∴∠ADE=∠BAF,
∵∠ADE+∠AEM=90°
∴∠EAM+∠AEM=90°
∴∠AME=90°
∴∠GND=90°
∴DE⊥CG.
∵∠AMD=90°,G点为AD中点,
∴DG=MG, DE⊥CG.
∴CG垂直平分DM,
∴CD=CM,
但是∠MDC不等于60°,所以
CD不等于DM故②错误;
在△GDC和△GMC中,
∵  ,
,

∴△GDC≌△GMC(SSS),
∴∠CDG=∠CMG=90°,∠MGC=∠DGC,
∴GM⊥CM,故①正确;
∵∠CDG=∠CMG=90°,
∴∠MGD+∠DCM=360°-∠CDG-∠CMG=180°
∵∠AGM+∠MGD=180°,
∴∠AGM=∠DCM,
∵CD=CM,
∴∠CMD=∠CDM,
在Rt△AMD中,∠AMD=90°,
∴DM<AD,
∴DM<CD,
∴∠DMC≠∠DCM,
∴∠CMD≠∠AGM,故④错误.
故选:B.