��Ŀ����
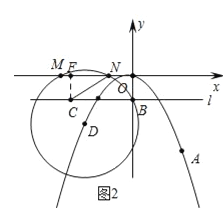
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У������߾�������ԭ��O����A��6����6![]() ��������y��Ϊ�Գ��ᣮ
��������y��Ϊ�Գ��ᣮ
��1���������ߵĽ���ʽ��
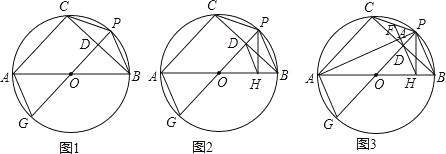
��2����ͼ2������B��0����![]() ����x���ƽ����l����C��ֱ��l�ϣ���D��y�������������ϣ�����DB���Ե�DΪԲ�ģ���DBΪ�뾶��Բ����D��x���ཻ�ڵ�M��N����M�ڵ�N����ࣩ������CN����MN=CNʱ���������MNC�Ķ�����
����x���ƽ����l����C��ֱ��l�ϣ���D��y�������������ϣ�����DB���Ե�DΪԲ�ģ���DBΪ�뾶��Բ����D��x���ཻ�ڵ�M��N����M�ڵ�N����ࣩ������CN����MN=CNʱ���������MNC�Ķ�����
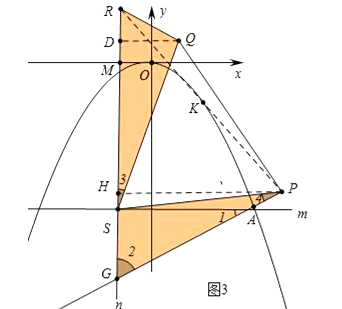
��3����ͼ3���ڣ�2���������£�ƽ��ֱ��CN������A�����������ཻ����һ��E������A��x���ƽ����m�����㣨��3��0����y���ƽ����n��ֱ��m��ֱ��n�ཻ�ڵ�S����R��ֱ��n�ϣ���P��EA���ӳ����ϣ�����SP����SPΪ���������ȱ���SPQ������RQ��PR������QRS=60�����߶�PR���е�Kǡ�������������ϣ���Q�����꣮

���𰸡���1��y=��![]() x2��
x2��
��2����CNF=30����
��3����Q��������![]() ��
��![]()
![]() ����
����
��������
�����������1���������ԭ��O����A��6����6![]() ��������y��Ϊ�Գ����������Ϊy=ax2����A�������a���ɣ�
��������y��Ϊ�Գ����������Ϊy=ax2����A�������a���ɣ�
��2����ͼ2�У���CF��MN��F������D��x��Ľ���Ϊ��x��0����D��m����![]() m2�������ݰ뾶����г����̣����M��N���꣬�Ƴ�MN=2
m2�������ݰ뾶����г����̣����M��N���꣬�Ƴ�MN=2![]() ����Rt��CFN�У���CN=2CF�Ƴ���FNC=30�����ɽ�����⣮
����Rt��CFN�У���CN=2CF�Ƴ���FNC=30�����ɽ�����⣮
��3����ͼ3�У��������֪ƽ��ֱ��CN������A��ֱ�ߵĽ���ʽΪy=![]() x��8
x��8![]() ����ֱ��y=
����ֱ��y=![]() x��8
x��8![]() ��ֱ��x=��3�Ľ���ΪG����G����3����9
��ֱ��x=��3�Ľ���ΪG����G����3����9![]() ��������SQR�ա�PSH���Ƴ�SR=PG��RQ=SG���Ƴ�RQ=SG=3
��������SQR�ա�PSH���Ƴ�SR=PG��RQ=SG���Ƴ�RQ=SG=3![]() ����DQ��n��D����n��x��Ľ���ΪM����RM=b����S����3����6
����DQ��n��D����n��x��Ľ���ΪM����RM=b����S����3����6![]() �����Ƴ�MS=6
�����Ƴ�MS=6![]() ���ɵ�P��6+
���ɵ�P��6+![]() b��
b��![]() b��6
b��6![]() ���������PR�е�k���֤꣬��k��ֱ��y=
���������PR�е�k���֤꣬��k��ֱ��y=![]() ��
��![]() ���˶�����
���˶����� ��ȥy�õ�x2+6x��27=0��x=3����9����������x=3������x=
��ȥy�õ�x2+6x��27=0��x=3����9����������x=3������x=![]() +
+![]() b�õ�b=2
b�õ�b=2![]() ���ɴ˼��ɽ�����⣮
���ɴ˼��ɽ�����⣮
�����������1���������ԭ��O����A��6����6![]() ��������y��Ϊ�Գ����������Ϊy=ax2��
��������y��Ϊ�Գ����������Ϊy=ax2��
����6![]() =36a��
=36a��
��a=��![]() ��
��
��y=��![]() x2��
x2��
��2����ͼ2�У���CF��MN��F������D��x��Ľ���Ϊ��x��0����D��m����![]() m2����
m2����
����x��m��2+��![]() m2��2=m2+����
m2��2=m2+����![]() m2+
m2+![]() ��2��
��2��
������x2��2mx+m2��3=0��
��x=m+![]() ��m��
��m��![]() ��
��
��N��m+![]() ��0����M��m��
��0����M��m��![]() ��0��
��0��
��MN=2![]() ��
��
��Rt��CFN�У��ߡ�CFN=90����CN=MN=2![]() ��CF=
��CF=![]() ��
��
��CN=2CF��
���CNF=30����
��3����ͼ3�У�
�������֪ƽ��ֱ��CN������A��ֱ�ߵĽ���ʽΪy=![]() x��8
x��8![]() ��
��
��ֱ��y=![]() x��8
x��8![]() ��ֱ��x=��3�Ľ���ΪG����G����3����9
��ֱ��x=��3�Ľ���ΪG����G����3����9![]() ����
����
��m��x�ᣬ�ҹ���A��6����6![]() ����
����
��S����3����6![]() ����
����
��SG=3![]() ��AS=9��
��AS=9��
��tan��2=![]() =
=![]() ��
��
���2=60����
���1=30����
�ߡ�QRS=60��
���QRS=��2��
�ߡ�RSQ+��QSP=��2+��SPG����QSP=��2=60����
���3=��4��
����SQR����PSG��
 ��
��
���SQR�ա�PSH
��SR=PG��RQ=SG��
��RQ=SG=3![]() ����DQ��n��D��
����DQ��n��D��
��QRD=60����
��DQ=![]() DR=
DR=![]() RQ=
RQ=![]() ��
��
��RD=![]() QR=
QR=![]() ��
��
��n�ǹ�����3��0����y��ƽ�е�ֱ�ߣ���R����3��b������n��x��Ľ���ΪM����RM=b��
��S����3����6![]() ����
����
��MS=6![]() ��
��
��SR=RM+MS=b+6![]() =PG����PH��n��H��
=PG����PH��n��H��
�ߡ�2=60����
��GH=![]() PG=
PG=![]() ��b+6
��b+6![]() ����
����
��MH=MG��HG=9![]() ��
��![]() ��b+6
��b+6![]() ��=6
��=6![]() ��
��![]() b��
b��
��P��6+![]() b��
b��![]() b��6
b��6![]() ����
����
��K��PR�е㣬
��K��![]() +
+![]() b��
b��![]() b��3
b��3![]() ����
����
Ϊ�˷��㣬��K��x��y������x=![]() +
+![]() b��y=
b��y=![]() b��3
b��3![]() ����ȥb��y=
����ȥb��y=![]() x��
x��![]()
![]() ��
��
���е�K��ֱ��y=![]() ��
��![]() ���˶���
���˶���
�� ��ȥy�õ�x2+6x��27=0��
��ȥy�õ�x2+6x��27=0��
��x=3����9����������
��x=3������x=![]() +b�õ�b=2
+b�õ�b=2![]() ��
��
��RM=2![]() ��DM=RM��RD=2
��DM=RM��RD=2![]() ��
��![]() =
=![]()
![]() ��
��
��![]() ��3=
��3=![]() ��
��
����Q��������![]() ��
��![]()
![]() ����
����

 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�����Ŀ��ij��ѧȥ��ͨ������Ʒ���ա���O�ʽ���������ƶ��ɽ���С�Сѧ����27������������һ����ѧ����ѧϰ������ҪxԪ������һ��Сѧ����ѧϰ������ҪyԪ�����꼶ѧ���O�ʽ���������ǡ�������С�Сѧ�������IJ���������±���
�꼶 | �O�ʽ����� | ����ƶ����ѧ | ����ƶ��Сѧ������������ |
���꼶 | 5000 | 2 | 5 |
���꼶 | 6000 | 3 | 5 |
���꼶 | 8000 |
��1����x��y��ֵ��
��2�����꼶ѧ���O���ʽ������������ƶ���С�Сѧ����ѧϰ���ã�������꼶ѧ��������ƶ���С�Сѧ��������