题目内容
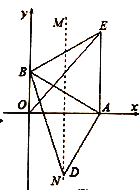
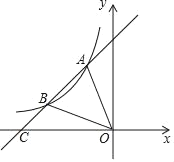
【题目】如图，一次函数y＝ax+b的图象与反比例函数y＝
图象相交于点A（﹣1，2）与点B（﹣4，n）．
（1）求一次函数和反比例函数的解析式；
（2）求△AOB的面积．
（3）在第二象限内，求不等式ax+b＜的解集（请直接写出答案）．
【答案】（1）y＝﹣
，y=
（2）
（3）﹣5＜x＜﹣4或﹣1＜x＜0
【解析】
（1）将点A（-1,2）代入反比例函数解析式即可求得反比例函数解析式，将两点代入一次函数即可求得一次函数解析式.
（2）求得C点的坐标后利用
求面积即可.
（3）根据图像即可得到结论.
（1）将点A（﹣1，2）代入函数y＝
，
解得：m＝﹣2，
∴反比例函数解析式为y＝﹣
，
将点A（﹣1，2）与点B（﹣4，
）代入一次函数y＝ax+b，
解得：a＝，b＝
∴一次函数的解析式为y＝
+；
（2）C点坐标（﹣5，0）
∴S△AOB＝S△AOC﹣S△BOC＝5﹣
＝；
（3）由图象知，不等式ax+b＜的解集为：﹣5＜x＜﹣4或﹣1＜x＜0．
练习册系列答案
阅读快车系列答案
相关题目
【题目】目前节能灯在城市已基本普及，今年山东省面向县级及农村地区推广节能灯，为响应号召，某商场计划购进甲、乙两种节能灯共1200只，这两种节能灯的进价、售价如下表：
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货，进货款恰好为46000元？
(2)如何进货，商场销售完节能灯时获利最多且不超过进货价的30%，此时利润为多少元？
